题目内容
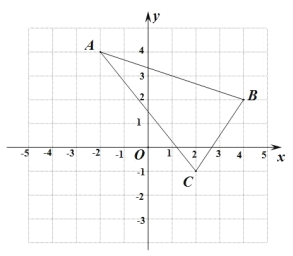
【题目】探究题:如图,AB⊥BC,射线CM⊥BC,且BC=5cm,AB=1cm,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=4cm,则CD= ;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,则CD= cm.(请直接写出答案)
【答案】(1)4cm;(2)PB=PC,理由见解析;(3)4
【解析】
(1)根据AAS定理证明△ABP≌△PCD,可得BP=CD;
(2)延长线段AP、DC交于点E,分别证明△DPA≌△DPE、△APB≌△EPC,根据全等三角形的性质解答;
(3)根据等腰直角三角形的性质计算.
解:(1)∵BC=5cm,BP=4cm,
∴PC=1cm,
∴AB=PC,
∵DP⊥AP,
∴∠APD=90°,
∴∠APB+∠CPD=90°,
∵∠APB+∠CPD=90°,∠APB+∠BAP=90°,
∴∠BAP=∠CPD,
在△ABP和△PCD中,
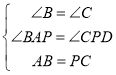 ,
,
∴△ABP≌△PCD,
∴BP=CD=4cm;
(2)PB=PC,
理由:如图2,延长线段AP、DC交于点E,
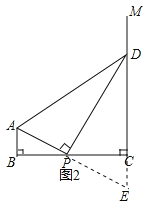
∵DP平分∠ADC,
∴∠ADP=∠EDP.
∵DP⊥AP,
∴∠DPA=∠DPE=90°,
在△DPA和△DPE中,
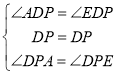 ,
,
∴△DPA≌△DPE(ASA),
∴PA=PE.
∵AB⊥BP,CM⊥CP,
∴∠ABP=∠ECP=Rt∠.
在△APB和△EPC中,
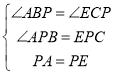 ,
,
∴△APB≌△EPC(AAS),
∴PB=PC;
(3)∵△PDC是等腰三角形,
∴△PCD为等腰直角三角形,即∠DPC=45°,
又∵DP⊥AP,
∴∠APB=45°,
∴BP=AB=1cm,
∴PC=BC﹣BP=4cm,
∴CD=CP=4cm,
故答案为:4.

 阅读快车系列答案
阅读快车系列答案【题目】一个不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同,某课外学习小组做摸球试验,将求搅均匀后从张任意摸出一个球,记下颜色后放回,搅匀,不断重复,获得数据如下
摸球次数 |
|
|
|
|
|
|
摸到白球的频数 |
|
|
|
|
|
|
摸到白球的频率 |
![]() 计算并填写表中摸到白球的频率;
计算并填写表中摸到白球的频率;
![]() 当摸球次数很大时,摸到的白球的频率估计值是多少?
当摸球次数很大时,摸到的白球的频率估计值是多少?
![]() 若已知袋中有白球
若已知袋中有白球![]() 个,试估计袋中红球的个数.
个,试估计袋中红球的个数.