题目内容
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于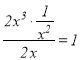 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于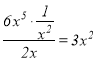 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于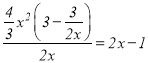 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于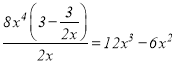 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: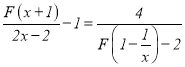 .
.
【答案】(1)是;(2)![]() ;(3)无解.
;(3)无解.
【解析】
(1)当A=![]() 时,F=2x3时,
时,F=2x3时,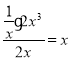 ;
;
(2)结合定义进行判断,即可求出F(A);
(3)结合定义即可求出F(x+1)=2x,F(1-![]() )=2x2,将所求方程转化为
)=2x2,将所求方程转化为![]() 即可求解.
即可求解.
(1)当A=![]() 时,F=2x3时,
时,F=2x3时,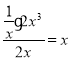
∴![]() 是2x3的整系单项式;
是2x3的整系单项式;
(2)∵![]()
∴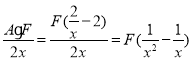
∵F(A)是A的系数最小的整系单项式,
∴![]() =
=![]() ;
;
(3) 易求F(x+1)=2x,F(1-![]() )=2x2,
)=2x2,
∴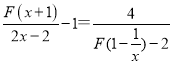 可以化为
可以化为![]() ,
,
∴x2-2x+1=0,
∴x=1;
经检验x=1是方程的增根,
∴原方程无解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目