题目内容
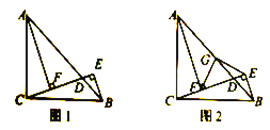
【题目】如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD

(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________ (用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE =6,求△ABC的面积.
【答案】(1)1:1;(2)m∶n;(3)9
【解析】
(1)过A作AE⊥BC于E,根据三角形面积公式求出即可;
(2)过D作DE⊥AB于E,DF⊥AC于F,根据角平分线性质求出DE=DF,根据三角形面积公式求出即可;
(3)根据已知和(1)(2)的结论求出△ABD和△ACD的面积,即可求出答案.
解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(![]() ×BD×AE):(
×BD×AE):(![]() ×CD×AE)=1:1,
×CD×AE)=1:1,
故答案为:1:1;

(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(![]() ×AB×DE):(
×AB×DE):(![]() ×AC×DF)=m:n;
×AC×DF)=m:n;

(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.


练习册系列答案
相关题目