题目内容
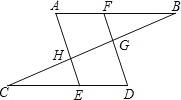
【题目】如图，已知平行四边形ABCO，以点O为原点，OC所在的直线为x轴，建立直角坐标系，AB交y轴于点D，AD=4，OC=10，∠A=60°，线段EF垂直平分OD，点P为线段EF上的动点，PM⊥x轴于点M点，点E与E'关于x轴对称，连接BP、E'M，则BP+PM+ME'的长度的最小值为______．
【答案】
【解析】
连接OP,先确定OD的长和B点坐标，然后证明四边形OPME'是平行四边形，可得OP=EM，因为PM是定值，推出PB+ME'=OP+PB的值最小时，即当O、P、B共线时BP+PM+M E的长度最小，最后根据两点间的距离公式和线段的和差解答即可．
解:如图：连接OP
在Rt△ADO中，∠A=60°，AD=4，
∴OD=4tan60°=4
，
∴A（-4，4）
∵四边形ABCD是平行四边形，
∴AB=OC=10，
∴DB=10-4=6
∴B（6，4）
∵线段EF垂直平分OD
∴OE=
OD=2，∠PEO=∠EOM=∠PM0=90°，
∴四边形OMPE是矩形，
∴PM=OE=2，
∵OE=0E'
∴PM=OE'，PM//OE'，
∴四边形OPME'是平行四边形，
∴0P=EM，
∵PM=2是定值，
∴PB+ME'=OP+PB的值最小时，BP+PM+ME的长度最小，
∴当0、P、B共线时，BP+PM+ME的长度最小
∴BP+PM+ME的最小值为OB+PM=
．
故答案为．
【题目】珠海市水务局对某小区居民生活用水情况进行了调査．随机抽取部分家庭进行统计，绘制成如下尚未完成的频数分布表和频率分布直方图．请根据图表，解答下列问题：
月均用水量（单位：吨 | 频数 | 频率 |
2≤x＜3 | 4 | 0.08 |
3≤x＜4 | a | b |
4≤x＜5 | 14 | 0.28 |
5≤x＜6 | 9 | c |
6≤x＜7 | 6 | 0.12 |
7≤x＜8 | 5 | 0.1 |
合计 | d | 1.00 |
（1）b= ，c= ，并补全频数分布直方图；
（2）为鼓励节约用水用水，现要确定一个用水量标准P（单位：吨），超过这个标准的部分按1.5倍的价格收费，若要使60%的家庭水费支出不受影响，则这个用水量标准P= 吨；
（3）根据该样本，请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户？
