题目内容
【题目】如图1，在
中，
，
，
与
相交于点
，且
，
，垂足分别为点
、
.
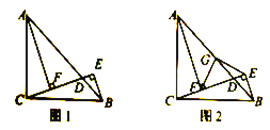
（1）若
，
，求
的长.
（2）如图2，取中点
，连接
、
，请判断
的形状，并说明理由.
【答案】（1）3；（2）
为等腰直角三角形
【解析】
（1）根据AAS只要证明△ACF≌△CBE，得到CE=AF=5，CF=BE=2，即可得到EF；
（2）连接CG，由（1）得到△ABC是等腰直角三角形，CG是中线，得到∠CBG=45°，得到CG=BG，易得到∠GCF=∠GBE，CF=BF，由SAS证明△CFG≌△BEG，得到FG=EG，∠CGF=∠BGE，再由等角互换得到∠FGE=∠AGC=90°，即可得到的形状为等腰直角三角形.
解：（1）∵
∴
∵
∴
∴
∴
∵
，∴
在
和△
中
∴
∴
∵
∴
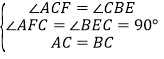
（2）为等腰直角三角形
理由如下：连接
∵
∴
，
∴
∴
∴
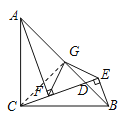
在
和
中
∵
，
∴
由（1）证可知：
∴
∵
∴
∴
∵
∴
∴
∵
∴
即
∴
是等腰直角三角形
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
