题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]()
![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 恰有一个公共点,结合函数图象,则
恰有一个公共点,结合函数图象,则![]() 的取值范围__________.
的取值范围__________.
【答案】![]() 或
或![]() 或
或![]()
【解析】
先根据直线的解析式求出点A,B的坐标,再求出点C的坐标,将点A的坐标代入抛物线,求出a和b的关系式为![]() ,从而可得抛物线的对称轴为
,从而可得抛物线的对称轴为![]() ,则抛物线与x轴的另一个交点为
,则抛物线与x轴的另一个交点为![]() ;需分
;需分![]() 和
和![]() 两种情况分析,再根据抛物线与线段BC恰有一个公共点建立不等式求解即可.
两种情况分析,再根据抛物线与线段BC恰有一个公共点建立不等式求解即可.
令![]() ,代入直线
,代入直线![]() 得:
得:![]() ,则点A的坐标为
,则点A的坐标为![]()
令![]() ,代入直线
,代入直线![]() 得:
得:![]() ,则点B的坐标为
,则点B的坐标为![]()
将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() ,则点C的坐标为
,则点C的坐标为![]()
将![]() 代入抛物线
代入抛物线![]() 得:
得:![]() ,即
,即![]()
则抛物线的解析式为![]() ,因此其对称轴为
,因此其对称轴为![]() ,与x轴的另一个交点的坐标为
,与x轴的另一个交点的坐标为![]()
由题意得![]() ,所以分以下两种情况讨论:
,所以分以下两种情况讨论:
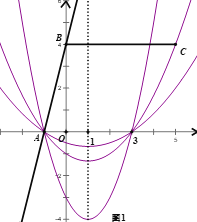
(1)如图1,当![]() 时,要使抛物线与线段BC恰有一个公共点
时,要使抛物线与线段BC恰有一个公共点
则当![]() 时,
时,![]() 才能符合题意,即
才能符合题意,即![]()
解得:![]()
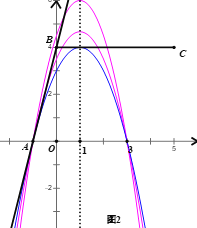
(2)如图2,当![]() 时,要使抛物线与线段BC恰有一个公共点,又需分两种情况:
时,要使抛物线与线段BC恰有一个公共点,又需分两种情况:
①抛物线的顶点恰好在线段BC上,此时公共点为抛物线的顶点,符合题意
则当![]() 时,
时,![]() ,即
,即![]()
解得:![]()
②抛物线的顶点在线段BC的上方,此时当![]() 时,
时,![]() 才能符合题意
才能符合题意
将![]() 代入抛物线得:
代入抛物线得:![]()
解得:![]()
综上,若抛物线与线段BC恰有一个公共点,a的取值范围为![]() 或
或![]() 或
或![]()
故答案为:![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
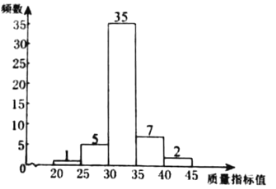
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)