题目内容
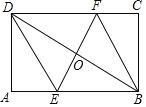
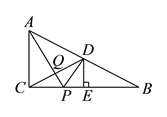
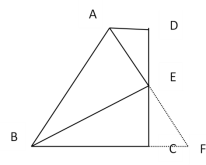
【题目】如图, 在四边形ABCD中,AD∥BC, E为CD的中点,连接 AE 、BE ,BE⊥AE, 延长AE交BC的延长线于 F,求证:(1) BE平分∠ABC (2)AB=BC+AD
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AD//BC可知∠DAE=∠F ,∠D=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质可得AE=EF ,AD=CF,由BE⊥AE可得∠AEB=∠FEB可证△ABE≌△FBE即可解答.
(2)由(1)知 AD=CF, △ABE≌△FBE,可判断出AB= BF,由BF=BC+CF=BC+AD即可证.
证明: 如图 延长AE交BC的延长线于 F,
(1)∵ AD∥BC
∴ ∠DAE=∠F ∠D=∠ECF
∵ E为CD中点
∴ DE=CE
∵在△ADE和△FCE中
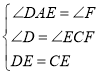
∴ △ADE≌△FCE (AAS)
∴ AE=EF,AD=CF
又∵ BE⊥AE
∴ ∠AEB=∠FEB=90°
∵在△ABE和△FBE中
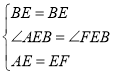
∴ △ABE≌△FBE (SAS)
∴∠ABE=∠FBE
则BE平分∠ABC
(2)由(1)知 AD=CF △ABE≌△FBE
∴AB=BF
∵BF=BC+CF
∴BF=BC+CF=BC+AD
∴AB=BC+AD

练习册系列答案
相关题目