Question

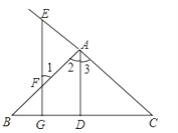
【题目】看图填空：已知如图，AD⊥BC于D，EG⊥BC于G，∠E=∠1，

求证：AD平分∠BAC．

证明：∵AD⊥BC于D，EG⊥BC于G（ 已知 ）

∴∠ADC=90°，∠EGC=90°（___________）

∴∠ADC=∠EGC（等量代换）

∴AD∥EG（_____________）

∴∠1=∠2（___________）

∠E=∠3（___________）

又∵∠E=∠1（ 已知）

∴∠2=∠3（___________）

∴AD平分∠BAC（___________）．

Answer 1

【答案】 垂直的定义； 同位角相等，两直线平行； 两直线平行，内错角相等； 两直线平行，同位角相等； 等量代换； 角平分线的定义

【解析】试题分析：由垂直可证明AD∥EG，由平行线的性质可得到∠1=∠2=∠3=∠E，可证得结论，据此填空即可．

证明：

∵AD⊥BC于D，EG⊥BC于G（已知），

∴∠ADC=90°，∠EGC=90°（垂直的定义），

∴∠ADC=∠EGC（等量代换），

∴AD∥EG（同位角相等，两直线平行），

∴∠1=∠2（两直线平行，内错角相等），

∠E=∠3（两直线平行，同位角相等），

又∵∠E=∠1（已知），

∴∠2=∠3（等量代换），

∴AD平分∠BAC（角平分线的定义）．

故答案为：垂直的定义；同位角相等，两直线平行；两直线平行，内错角相等；两直线平行，同位角相等；等量代换；角平分线的定义．