题目内容
【题目】在平面直角坐标系xOy中,抛物线c1:y=ax2﹣4a+4(a<0)经过第一象限内的定点P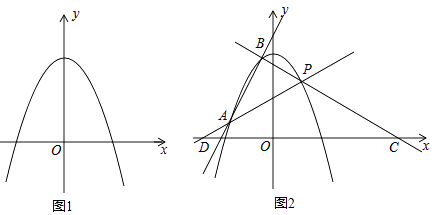
(1)直接写出点P的坐标;
(2)若a=﹣1,如图1,点M的坐标为(2,0)是x轴上的点,N为抛物线c1上的点,Q为线段MN的中点,设点N在抛物线c1上运动时,Q的运动轨迹为抛物线c2 , 求抛物线c2的解析式;
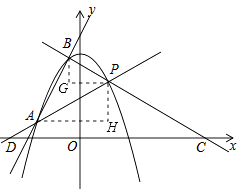
(3)直线y=2x+b与抛物线c1相交于A、B两点,如图2,直线PA、PB与x轴分别交于D、C两代女.当PD=PC时,求a的值.
【答案】
(1)解:∵y=ax2﹣4a+4=a(x2﹣4)+4,该函数图象过第一象限内的定点P,
∴x2﹣4=0,
解得 x=2或x=﹣2(舍去),
则y=4,
∴点P的坐标是(2,4)
(2)解:设点Q的坐标为(xQ,yQ),点N的坐标为(xN,yN).
∵M(2,0).
由点Q是线段MN的中点,可以求得,xN=2xQ﹣2,yN=2yQ.
∵a=﹣1,
∴抛物线c1的解析式为y=﹣x2+8.
∵点N在抛物线c1上,
∴yN=﹣xN2+8.
∴2yQ=﹣(2xQ﹣2)2+8,即yQ=﹣2xQ2+4xQ+2,
∴抛物线c2的解析式为:y=﹣2x2+4x+2.
(3)解:设点A、B的坐标分别为A(x1,ax12﹣4a+4)、B(x2,ax22﹣4a+4).
又∵点A、B在直线y=2x+b上,
∴a(x1+x2)=2.
如图,过点B作BG∥y轴,过点P作PG∥x轴,BG、PG相交于点G,过点A作AH∥x轴,过点P作PH∥y轴,AH、PH相交于点H.
∵PD=PC,
∴∠PDC=∠PCD.
∵AH∥x轴,
∴∠PAH=∠PDC.
同理,∠BPG=∠PCD,
∴∠AHP=∠PGB,
∴Rt△PGB∽Rt△AHP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴x1+x2=﹣4,
∴a=﹣ ![]() .
.
【解析】本题考查了待定系数法求二次函数解析式、相似三角形的判定与性质、二次函数图象上点的坐标特征等知识. 解答第(2)题的技巧在于用点Q的坐标表示点N的坐标,然后把点N的坐标代入其所在的抛物线的解析式,通过化简可求得抛物线c2的解析式.