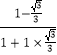题目内容
【题目】一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
A种水果/箱 | B种水果/箱 | |
甲店 | 11元 | 17元 |
乙店 | 9元 | 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
【答案】
(1)解:经销商能盈利=5×11+5×17+5×9+5×13=5×50=250
(2)解:设甲店配A种水果x箱,则甲店配B种水果(10﹣x)箱,
乙店配A种水果(10﹣x)箱,乙店配B种水果10﹣(10﹣x)=x箱.
∵9×(10﹣x)+13x≥100,
∴x≥2 ![]() ,
,
经销商盈利为w=11x+17(10﹣x)+9(10﹣x)+13x=﹣2x+260.
∵﹣2<0,
∴w随x增大而减小,
∴当x=3时,w值最大.
甲店配A种水果3箱,B种水果7箱.乙店配A种水果7箱,B种水果3箱.最大盈利:﹣2×3+260=254(元).
【解析】(1)分别计算两种水果的盈利相加即可;(2)由“乙店盈利不小于100元“可构建不等式9×(10﹣x)+13x≥100,最值问题可构造函数,求出x的范围,在此范围内按函数的单调性求出最值.
【考点精析】利用正比例函数的图象和性质对题目进行判断即可得到答案,需要熟知正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦.

练习册系列答案
相关题目