题目内容
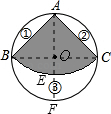
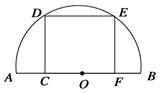
(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径? (3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
(1)50π(2)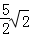 (3)不能,理由见解析
(3)不能,理由见解析
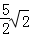 (3)不能,理由见解析
(3)不能,理由见解析(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=10 ,
,
∴S扇形=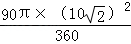 =50π﹣﹣﹣﹣﹣﹣(2分)
=50π﹣﹣﹣﹣﹣﹣(2分)
(2)圆锥侧面展开图的弧长为: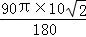 =5
=5 ,
,
∴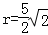 ﹣﹣﹣﹣﹣﹣(3分)
﹣﹣﹣﹣﹣﹣(3分)
(3)延长AO交⊙O于点F,交扇形于点E,EF=20﹣10 ,最大半径为10﹣5
,最大半径为10﹣5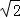 <r,
<r,
∴不能﹣﹣﹣﹣﹣﹣(3分)
(1)连接BC,易得AB的长,利用扇形的面积公式可得最大直角扇形的面积;
(2)易得扇形的弧长,除以2π即为圆锥底面圆的半径;
(3)算出余料中能取得圆的最大直径,进而求得最大半径,与(2)中圆锥的底面半径比较,看是否符合即可.

∵∠BAC=90°,AB=AC,
∴AB=AC=10
 ,
,∴S扇形=
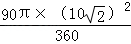 =50π﹣﹣﹣﹣﹣﹣(2分)
=50π﹣﹣﹣﹣﹣﹣(2分)(2)圆锥侧面展开图的弧长为:
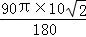 =5
=5 ,
,∴
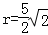 ﹣﹣﹣﹣﹣﹣(3分)
﹣﹣﹣﹣﹣﹣(3分)(3)延长AO交⊙O于点F,交扇形于点E,EF=20﹣10
 ,最大半径为10﹣5
,最大半径为10﹣5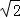 <r,
<r,∴不能﹣﹣﹣﹣﹣﹣(3分)
(1)连接BC,易得AB的长,利用扇形的面积公式可得最大直角扇形的面积;
(2)易得扇形的弧长,除以2π即为圆锥底面圆的半径;
(3)算出余料中能取得圆的最大直径,进而求得最大半径,与(2)中圆锥的底面半径比较,看是否符合即可.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
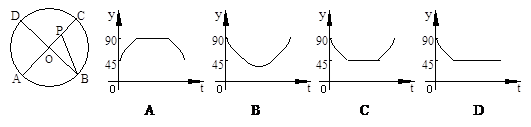

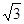 D、10+
D、10+