题目内容
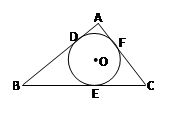
已知如图,△ABC外切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
A、12 B、14 C、10+2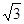 D、10+
D、10+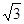

A、12 B、14 C、10+2
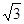 D、10+
D、10+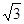
C
如图,连接OE、OF、OC,
∵∠C=60°,
∴∠OCE=30°,
∵OE=1,
∴OC=2,CE= ,
,
∴CF= ,
,
∵△ABC内切⊙O于D、E、F三点,
∴BD=BE,AD=AF,
∵AB=5,
∴AD+BD=AF+BE=5,
∴△ABC的周长=AD+BD+AF+BE+CD+CE,
=5+5+2 ,
,
=10+2 .
.
故选C.

∵∠C=60°,
∴∠OCE=30°,
∵OE=1,
∴OC=2,CE=
 ,
,∴CF=
 ,
,∵△ABC内切⊙O于D、E、F三点,
∴BD=BE,AD=AF,
∵AB=5,
∴AD+BD=AF+BE=5,
∴△ABC的周长=AD+BD+AF+BE+CD+CE,
=5+5+2
 ,
,=10+2
 .
.故选C.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
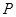 为正比例函数
为正比例函数 图象上的一个动点,⊙P的半径为
图象上的一个动点,⊙P的半径为 ,当⊙P与直线
,当⊙P与直线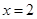 相切时,则点
相切时,则点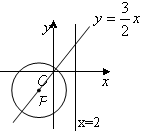
 、⊙
、⊙ 外切于点
外切于点 ,经过点
,经过点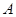 、
、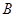 ,
,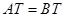 ;
;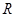 、
、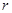 (如图2),试写出线段
(如图2),试写出线段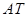 、
、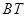 与
与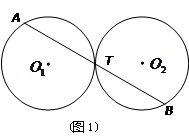
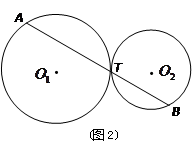
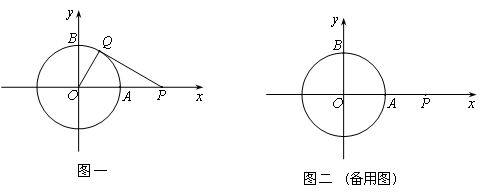
 的切线,连接OQ.求
的切线,连接OQ.求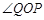 的大小;
的大小;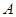 、
、 、
、 是⊙O上的三点,
是⊙O上的三点,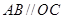 .
.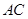 平分
平分 .
.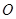 作
作 于点
于点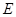 ,交
,交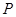 . 若
. 若 ,
,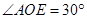 ,求
,求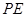 的长. )
的长. )