题目内容
【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( ) 
A.3
B.4
C.2 ![]()
D.![]()
【答案】C
【解析】解:过点D作DE⊥AB交AB于E, 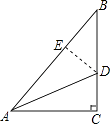
设CD=x,则BD=8﹣x,
∵AD平分∠BAC,
∴ ![]() ,即
,即 ![]() ,
,
∴x=3,
∴CD=3,
∴S△ABD= ![]() ABDE=
ABDE= ![]() 3=15,
3=15,
∵AD= ![]() =3
=3 ![]() ,
,
设BD到AD的距离是h,
∴S△ABD= ![]() ADh,
ADh,
∴h=2 ![]() .
.
故选C.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目