题目内容
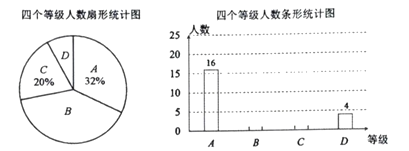
【题目】在达州市关工委组织的“五好小公民”主题教育活动中,我市某中学组织全校学生参加了“红旗队飘,引我成长”知识竞赛,赛后机抽取了部分参赛学生的成绩,从高分到低分将成绩分成![]() 五类,绘制成下面两个不完整的统计图:
五类,绘制成下面两个不完整的统计图:
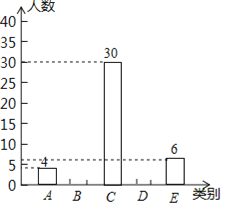
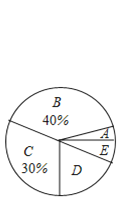
根据上面提供的信息解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生4200人,求成绩为![]() 类的学生人数和
类的学生人数和![]() 类学生所对应的圆心角的度数;
类学生所对应的圆心角的度数;
(3)若![]() 类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
【答案】(1)图详见解析;(2)840,72°;(3)![]()
【解析】
(1)首先用C类别的学生人数除以C类别的人数占的百分率,求出共调查多少名学生;然后根据B类别百分比求得其人数,由各类别人数和等于总人数求得D的人数,即可补全统计图;
(2)用全校人数乘以D类别人数所占比例即可得到成绩为![]() 类的学生人数,用360
类的学生人数,用360![]() 乘以样本中D类别人数所占比例可得其圆心角度数;
乘以样本中D类别人数所占比例可得其圆心角度数;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名担任校园广播“孝心伴我行”节目主持人,应用列表法的方法,求出恰好选到1名男生和1名女生的概率是多少即可.
解:(1)∵被调查的总人数为30÷30%=100人,则B类别人数为100×40%=40人,
∴D类别人数为100﹣(4+40+30+6)=20人,
补全条形图如下:
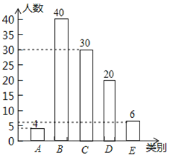
(2)D类的学生人数:4200×(20÷100)=840(人),
D类所对应的圆心角是![]()
(3)列表为:
男1 | 男2 | 女1 | 女2 | |
男1 | ﹣﹣ | 男2男1 | 女1男1 | 女2男1 |
男2 | 男1男2 | ﹣﹣ | 女1男2 | 女2男2 |
女1 | 男1女1 | 男2女1 | ﹣﹣ | 女2女1 |
女2 | 男1女2 | 男2女2 | 女1女2 | ﹣﹣ |
由上表可知,从4名学生中任意选取2名学生共有12种等可能结果,其中恰好选到1名男生和1名女生的结果有8种,
∴恰好选到1名男生和1名女生的概率为![]() .
.