Question

【题目】菱形ABCD的边长为4cm,∠A=120°，则菱形ABCD的面积为______．

Answer 1

【答案】8cm

【解析】

根据已知条件和菱形的性质易证△ABC为等边三角形，即可得AC=AB=4cm．由此求得OA=2cm，在直角△AOB为中，根据勾股定理求得的OB= cm，即可得BD=4cm，由菱形的面积等于对角线乘积的一半即可求解.

在菱形ABCD中，∠BAC=∠BAD=×120°=60°，AB=BC，AC⊥BD，OA=OC，OB=OD，

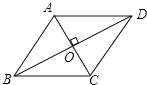
又∵在△ABC中，AB=BC，

∴△ABC为等边三角形，

∴AC=AB=4cm．

∴OA=2cm，

在直角△AOB为中，根据勾股定理求得的OB= cm，

∴BD=2BO=4cm，

∴菱形ABCD的面积为： AC×BD=×4×4=8 cm.

故答案为：8 cm．