Question

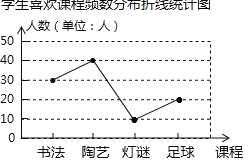
【题目】某校校本课程中心为了解该校学生喜欢校本课程的情况，采取抽样调查的办法，通过书法、陶艺、灯谜、足球四门课程的选报情况调查若干名学生的兴趣爱好，要求每位同学只能选择一门自己喜欢的课程，并将调查结果绘制成如下两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

（1）在这次调查研究中，一共调查了　 　名学生，喜欢灯谜的人数在扇形统计图中所占的圆心角是　 　度：

（2）请补全频数分布折线统计图；

（3）为了平衡各校本课程的人数，需要从喜欢陶艺课程的甲、乙、丙3人中调整2人到灯谜课程，试用列表或树状图的方法求“甲、乙两人被同时调整到灯谜课程”的概率．

Answer 1

【答案】（1）100，36；（2）详见解析；（3）．

【解析】

（1）“陶艺”的有40人占调查人数的40%，即可求出调查人数，进而求出“书法”所占的百分比，“灯谜”所占的百分比，从而求出“灯谜”对应的圆心角度数；

（2）求出“灯谜”的人数，“足球”的人数即可补全统计图；

（3）用列表法列举出所有可能出现的情况，从中找出“甲乙被同时选中”的情况，求出概率即可．

（1）40÷40%＝100人，30÷100＝30%，360°×（1﹣20%﹣40%﹣30%）＝36°，

故答案为：100，36；

（2）足球人数：100×20%＝20人，灯谜人数为100﹣40﹣30﹣20＝10人，补全频数分布折线统计图如图所示：

（3）用列表法表示所有可能出现的情况如下：

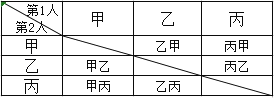
共有6种可能出现的情况，其中甲乙被同时选中的有2种，

∴P（甲乙同时被选中）＝；

答：甲、乙两人被同时选中的概率为．