题目内容
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
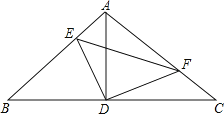
A.△ADF≌△BDE
B.S四边形AEDF=![]() S△ABC
S△ABC
C.BE+CF=![]() AD
AD
D.EF=AD
【答案】D
【解析】
试题分析:根据等腰直角三角形的性质得到AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,根据余角的性质得到∠BDE=∠ADF,于是得到△ADF≌△BDE,证得S△ADF=S△BDE,推出S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE﹣S△ABD,得到S四边形AEDF=![]() S△ABC,根据全等三角形的性质得到AF=BE,等量代换得到BE+CF=AF+CF=AC=
S△ABC,根据全等三角形的性质得到AF=BE,等量代换得到BE+CF=AF+CF=AC=![]() AD,由等腰直角三角形的性质得到AD=
AD,由等腰直角三角形的性质得到AD=![]() BC,当EF∥BC时,EF=
BC,当EF∥BC时,EF=![]() BC,而EF不一定平行于BC,即可得到结论.
BC,而EF不一定平行于BC,即可得到结论.
解:∵∠BAC=90°,AB=AC,点D为BC的中点,
∴AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,
∵∠EDF=90°,
∴∠BDE+∠ADE=∠ADE+∠ADF=90°,
∴∠BDE=∠ADF,
在△ADF与△BDE中,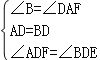 ,
,
∴△ADF≌△BDE,
∴S△ADF=S△BDE,
∵S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE﹣S△ABD,
∵S△ABD=![]() S△ABC,
S△ABC,
∴S四边形AEDF=![]() S△ABC,
S△ABC,
∵△ADF≌△BDE,
∴AF=BE,
∴BE+CF=AF+CF=AC=![]() AD,
AD,
∵AD=![]() BC,
BC,
当EF∥BC时,EF=![]() BC,
BC,
而EF不一定平行于BC,
∴EF不一定等于![]() BC,
BC,
∴EF≠AD,
故选D.

练习册系列答案
相关题目