题目内容
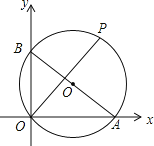
【题目】如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
A.(8,6) B.(7,7) C.(7![]() ,7
,7![]() ) D.(5
) D.(5![]() ,5
,5![]() )
)
【答案】B
【解析】
试题分析:作PH⊥x轴于H,连结PA、PB,由A、B两点的坐标可求出AB,由△PAB和△POH都为等腰直角三角形,得出PA=![]() AB,PH=OH,设OH=t,在在Rt△PHA中,运用勾股定理求出t的值,即可得出点P的坐标.
AB,PH=OH,设OH=t,在在Rt△PHA中,运用勾股定理求出t的值,即可得出点P的坐标.
解:如图,作PH⊥x轴于H,连结PA、PB,
∵∠AOB=90°,
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵A、B两点的坐标分别为(8,0)、(0,6),
∴OA=8,OB=6,
∴AB=![]() =10,
=10,
∵∠AOP=45°,
∴∠ABP=45°,
∴△PAB和△POH都为等腰直角三角形,
∴PA=![]() AB=5
AB=5![]() ,PH=OH,
,PH=OH,
设OH=t,则PH=t,AH=8﹣t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8﹣t)2=(5![]() )2,
)2,
解得t1=7,t2=1(舍去),
∴P点坐标为(7,7).
故选B.
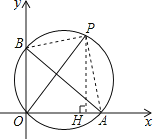

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?