题目内容
如图:在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,与两坐标轴交点为点A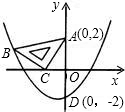 和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).
和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
 和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).
和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).(1)求抛物线的解析式;
(2)求点C的坐标;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
(1)将(-3,1),(0,-2)代入得:
解得
,
∴抛物线的解析式为:y=
x2+
x-2;
(2)过B作BE⊥x轴于E,则E(-3,0),
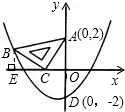 易证△BEC≌△COA,
易证△BEC≌△COA,
∴BE=AO=2,EB=CO=1,
∴C(-1,0);
(3)延长BC到P,使CP=BC,连接AP,
则△ACP为以AC为直角边的等腰直角三角形
过P作PF⊥x轴于F,易证△BEC≌△PFC,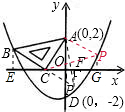
∴CF=CE=2PF=BE=1,
∴P(1,-1),
将(1,-1)代入抛物线的解析式满足;
若∠CAP=90°,AC=AP,
则四边形ABCP为平行四边形,
过P作PG⊥x轴于G,易证△PGA≌△CEB,
∴PG=2AG=1,
∴P(2,1)在抛物线上,
∴存在P(1,-1),(2,1)满足条件.
|
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过B作BE⊥x轴于E,则E(-3,0),
 易证△BEC≌△COA,
易证△BEC≌△COA,∴BE=AO=2,EB=CO=1,
∴C(-1,0);
(3)延长BC到P,使CP=BC,连接AP,
则△ACP为以AC为直角边的等腰直角三角形
过P作PF⊥x轴于F,易证△BEC≌△PFC,

∴CF=CE=2PF=BE=1,
∴P(1,-1),
将(1,-1)代入抛物线的解析式满足;
若∠CAP=90°,AC=AP,
则四边形ABCP为平行四边形,
过P作PG⊥x轴于G,易证△PGA≌△CEB,
∴PG=2AG=1,
∴P(2,1)在抛物线上,
∴存在P(1,-1),(2,1)满足条件.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 两点的抛物线的解析式.
两点的抛物线的解析式.