题目内容
如图:在⊙ 中
中 ,
, 则⊙
则⊙ 的周长是 。
的周长是 。 
 中
中 ,
, 则⊙
则⊙ 的周长是 。
的周长是 。 
根据圆周角定理,得∠A=∠BDC=60°,从而判断△ABC是等边三角形,再根据等边三角形的性质求得其外接圆的直径,从而求得其周长.
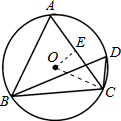
解:连接OC,作OE⊥AC于E.
∵∠ACB=∠BDC=60°,
∴∠A=∠BDC=60°,
∴△ABC是等边三角形,
∴∠OCE=30°,CE=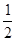 AC=
AC=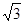 (垂径定理),
(垂径定理),
∴OC=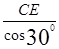 =2,
=2,
则⊙O的周长是4π.
故答案为4π.
此题考查了圆周角定理、等边三角形的判定及性质.
注意:等边三角形的外心和内心重合,是它的三边垂直平分线的交点.

解:连接OC,作OE⊥AC于E.
∵∠ACB=∠BDC=60°,
∴∠A=∠BDC=60°,
∴△ABC是等边三角形,
∴∠OCE=30°,CE=
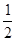 AC=
AC=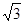 (垂径定理),
(垂径定理),∴OC=
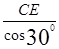 =2,
=2,则⊙O的周长是4π.
故答案为4π.
此题考查了圆周角定理、等边三角形的判定及性质.
注意:等边三角形的外心和内心重合,是它的三边垂直平分线的交点.

练习册系列答案
相关题目
 足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.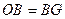 ,求证:四边形OCBD是菱形.
,求证:四边形OCBD是菱形.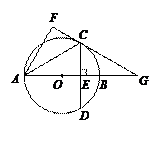

 ,扇形半径为R,则R与
,扇形半径为R,则R与
 图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,
图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3, 线于点M.
线于点M.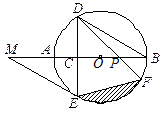
 ,则sin∠CBD的值等于( )
,则sin∠CBD的值等于( )

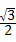

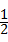

 ,
,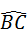 上分别取点E、F,使∠AO1E=∠BO2F
上分别取点E、F,使∠AO1E=∠BO2F ,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;
,则有结论①△PO1E≌△FO2P,②四边形PO1CO2是菱形,请给出结论②的证明;