题目内容
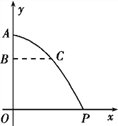
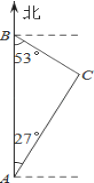
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
【答案】27.5海里/时
【解析】
先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(99-x)海里,在Rt△BCD中,根据tan53°=![]() ,求出CD,再根据
,求出CD,再根据![]() x=
x=![]() (121-x),求出BD,在Rt△BCD中,根据cos53°=
(121-x),求出BD,在Rt△BCD中,根据cos53°=![]() ,求出BC,从而得出答案.
,求出BC,从而得出答案.
解:如图,根据题意可得,在△ABC中,AB=121海里,∠ABC=53°,∠BAC=27°,点C作CD⊥AB,垂足为点D.
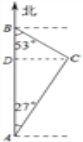
设BD=x海里,则AD=(121﹣x)海里,
在Rt△BCD中,tan53°=![]() ,则tan27°=
,则tan27°=![]() ,
,
CD=xtan53°≈![]() (海里).
(海里).
在Rt△ACD中,则CD=ADtan27°≈![]() (121﹣x),
(121﹣x),
则![]() =
=![]() (121﹣x),
(121﹣x),
解得,x=33, 即BD=33.
在Rt△BCD中,cos53°=![]() ,
,
则BC=![]() =55,
=55,
55÷2=27.5(海里/时),
则该可疑船只的航行速度约为27.5海里/时.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目