题目内容
如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过P点作⊙O的切线,切点为C,连接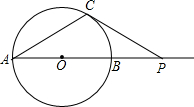 AC.
AC.(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M,你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP的值.
分析:(1)连接OC,根据切线的性质可知OC⊥PC,则△OPC为直角三角形,OC=3,可根据锐角三角函数的定义求出PC的值;
(2)从PM是∠APC的角平分线可知∠CPM=∠MPA,根据等腰三角形的性质及三角形内角和定理即可求出∠CMP=∠A+∠MPA=45度.因为∠A与∠CPA为定值,故∠CMP的大小不发生变化.
(2)从PM是∠APC的角平分线可知∠CPM=∠MPA,根据等腰三角形的性质及三角形内角和定理即可求出∠CMP=∠A+∠MPA=45度.因为∠A与∠CPA为定值,故∠CMP的大小不发生变化.
解答: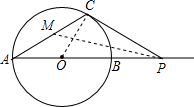 解:(1)连接OC,PM,
解:(1)连接OC,PM,
PC是⊙O的切线,
∴∠OCP=90°;
∵∠CPA=30°,OC=
=3,
∴tan30°=
=
,即PC=3
;(5分)
(2)∠CMP的大小不发生变化;(2分)
∵PM是∠CPA的平分线,
∴∠CPM=∠MPA,
∵OA=OC,
∴∠A=∠ACO;
在△APC中,
∵∠A+∠ACP+∠CPA=180°,
∴2∠A+2∠MPA=90°,∠A+∠MPA=45°,
∴∠CMP=∠A+∠MPA=45°; (5分)
即∠CMP的大小不发生变化,为45°.
 解:(1)连接OC,PM,
解:(1)连接OC,PM,PC是⊙O的切线,
∴∠OCP=90°;
∵∠CPA=30°,OC=
| AB |
| 2 |
∴tan30°=
| 3 |
| PC |
| ||
| 3 |
| 3 |
(2)∠CMP的大小不发生变化;(2分)
∵PM是∠CPA的平分线,
∴∠CPM=∠MPA,
∵OA=OC,
∴∠A=∠ACO;
在△APC中,
∵∠A+∠ACP+∠CPA=180°,
∴2∠A+2∠MPA=90°,∠A+∠MPA=45°,
∴∠CMP=∠A+∠MPA=45°; (5分)
即∠CMP的大小不发生变化,为45°.
点评:本题需要学生通过尝试,提出猜想、验证猜想、总结规律.既考查基本的数学知识与方法,又注重从特殊到一般的数学归纳能力的要求,突出了学生对图形的探究及探索出有效的解法策略.
[常见错误]
(1):利用三角函数解直角三角形时,三角函数与边不对应,或三角函数值记错;
(2):关于∠CMP的定值问题错误的两种观点:①认为∠CMP大小不变者,用第(1)小题的特殊值(∠A=30°)进行论证;②认为∠CMP大小变化者,把∠A看成是不变的角(30°),∠CMP=∠A+∠CMP=30°+∠CMP.
[常见错误]
(1):利用三角函数解直角三角形时,三角函数与边不对应,或三角函数值记错;
(2):关于∠CMP的定值问题错误的两种观点:①认为∠CMP大小不变者,用第(1)小题的特殊值(∠A=30°)进行论证;②认为∠CMP大小变化者,把∠A看成是不变的角(30°),∠CMP=∠A+∠CMP=30°+∠CMP.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
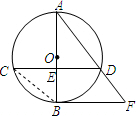 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
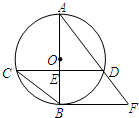 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于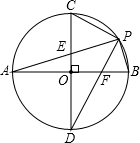 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: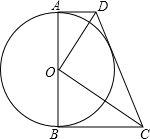 (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=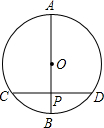 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是