题目内容
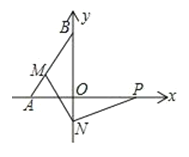
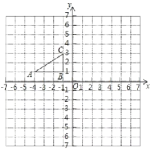
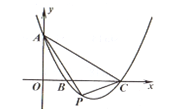
【题目】如图,平面直角坐标系中,抛物线y=-![]() x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A. 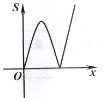 B.
B.  C.
C. 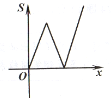 D.
D. 
【答案】B
【解析】解方程![]() 得B(2,0),C(6,0),易得点A的坐标为(0,3),利用对称性得到抛物线与直线 y=3的另一交点坐标(8,3),利用待定系数法可求出直线AC的解析式为y=
得B(2,0),C(6,0),易得点A的坐标为(0,3),利用对称性得到抛物线与直线 y=3的另一交点坐标(8,3),利用待定系数法可求出直线AC的解析式为y=![]() ,过点P作PD∥y轴交AC于D,如图,设点P的坐标为(x,
,过点P作PD∥y轴交AC于D,如图,设点P的坐标为(x,![]() ),则点D的坐标为(x,
),则点D的坐标为(x,![]() ),讨论:当0≤x≤6时,S=
),讨论:当0≤x≤6时,S=![]() ;当6<x≤8时,S=
;当6<x≤8时,S=![]() .
.
当y=0时,![]() ,解得
,解得![]() =2,
=2,![]() =6,∴点B的坐标为(2,0),点C的坐标为(6,0);当x=0时,y=
=6,∴点B的坐标为(2,0),点C的坐标为(6,0);当x=0时,y=![]() ,则点A的坐标为(0,3),抛物线的对称轴为直线x=4,点A关于直线x=4的对称点为(8,3),利用待定系数法可求出直线AC的解析式为y=-
,则点A的坐标为(0,3),抛物线的对称轴为直线x=4,点A关于直线x=4的对称点为(8,3),利用待定系数法可求出直线AC的解析式为y=-![]() ,过点P作PD∥y轴交AC于D,如图,设点P的坐标为(x,
,过点P作PD∥y轴交AC于D,如图,设点P的坐标为(x,![]() ),则点D的坐标为(x,
),则点D的坐标为(x,![]() ),当0≤x≤6时,
),当0≤x≤6时,
∴DP=![]() ,∴S=
,∴S=![]() ,
,
当6<x≤8时,∴DP=![]() ,∴S=
,∴S=![]() ,
,
故选B.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目