题目内容
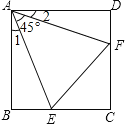
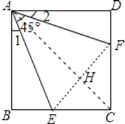
【题目】如图,已知正方形ABCD边长为1,![]() ,
,![]() ,则有下列结论:①
,则有下列结论:①![]() ;②点C到EF的距离是2-1;③
;②点C到EF的距离是2-1;③![]() 的周长为2;④
的周长为2;④![]() ,其中正确的结论有( )
,其中正确的结论有( )
A.4个B.3个C.2个D.1个
【答案】C
【解析】
先证明Rt△ABE≌Rt△ADF得到∠1=∠2,易得∠1=∠2=∠22.5°,于是可对①进行判断;连接EF、AC,它们相交于点H,如图,利用Rt△ABE≌Rt△ADF得到BE=DF,则CE=CF,接着判断AC垂直平分EF,AH平分∠EAF,于是利用角平分线的性质定理得到EB=EH,FD=FH,则可对③④进行判断;设BE=x,则EF=2x,CE=1-x,利用等腰直角三角形的性质得到2x=![]() (1-x),解方程,则可对②进行判断.
(1-x),解方程,则可对②进行判断.
解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连接EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
∵AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CE+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1-x,
∵△CEF为等腰直角三角形,
∴EF=![]() CE,即2x=
CE,即2x=![]() (1-x),解得x=
(1-x),解得x=![]() -1,
-1,
∴BE=![]() -1,
-1,
Rt△ECF中,EH=FH,
∴CH=![]() EF=EH=BE=
EF=EH=BE=![]() -1,
-1,
∵CH⊥EF,
∴点C到EF的距离是![]() -1,
-1,
所以②错误;
本题正确的有:①③;
故选:C.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目