��Ŀ����
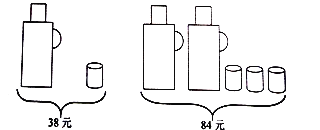
����Ŀ����ͼ1������![]() ��
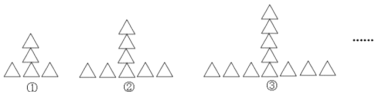
��![]() ���ڲ���ͼ�й���3���ǣ�
���ڲ���ͼ�й���3���ǣ�![]() ��
��![]() ��
��![]() ����������һ���ǵĶ�������һ���Ƕ������������������
����������һ���ǵĶ�������һ���Ƕ������������������![]() ��
��![]() �������ߣ�
�������ߣ�
��1����ͼ1����![]() ���ڲ���
���ڲ���![]() ��_________�������ߣ�
��_________�������ߣ�
��2����ͼ2����![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��
��![]() λ�ÿ�ʼ����ÿ��
λ�ÿ�ʼ����ÿ��![]() ���ٶ���ʱ����ת����
���ٶ���ʱ����ת����![]() �״ε���
�״ε���![]() ʱֹͣ��ת������ת��ʱ��Ϊ
ʱֹͣ��ת������ת��ʱ��Ϊ![]() ��
��
��ֱ��д����![]() Ϊ��ֵʱ������
Ϊ��ֵʱ������![]() ��
��![]() �������ߣ�
�������ߣ�
��������![]() ͬʱ�Ƶ�
ͬʱ�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ���ʱ����ת������
���ٶ���ʱ����ת������![]() ͬʱֹͣ��ת�������������
ͬʱֹͣ��ת�������������![]() ��
��![]() ��������ʱ
��������ʱ![]() ��ֵ��
��ֵ��
���𰸡���1��3����2����tΪ4.5��6��9 ����![]() ��
��![]() ��
��![]()
��������
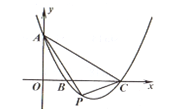
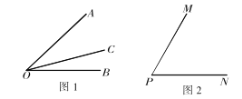
��1�����������ߵĶ��壬��OC������![]() ��
��![]() �������ߣ��С�AOB=2��AOC����AOC=2��BOC����BOC=2��AOC���������
�������ߣ��С�AOB=2��AOC����AOC=2��BOC����BOC=2��AOC���������
��2���ٱ������QPN����QPM=20��t-60�����ٷ�������������������ߵĶ����г����̼�����⣻
�ڱ������QPN����M��PN����M��PQ���ٷ�������������������ߵĶ����г����̼�����⣻
�⣺��1������AOB=2��AOC����OC������![]() ��
��![]() �������ߣ�
�������ߣ�
����AOC=2��BOC����OC������![]() ��
��![]() ��������
��������
����BOC=2��AOC����OC������![]() ��
��![]() ��������
��������
����![]() ���ڲ���
���ڲ���![]() ��3�������ߣ�
��3�������ߣ�
�ʴ�Ϊ��3��
��2���١ߡ�QPN=20��t����MPN=60��
���QPM=20��t-60��
����QPN=2��MPNʱ����20��t=120�������t=6s��
����QPM=2��MPNʱ����20��t-60��=120�������t=9s��
����MPN=2��QPMʱ����60��=2��20��t-60���������t=4.5s��
�ʴ�Ϊ��tΪ4.5��6��9��
����������QPN=20��t����M��PN=60��+12��t����M��PQ=60��-8��t
��![]() ʱ
ʱ
��![]()
��![]()
��![]() ʱ��
ʱ��
��![]()
��![]()
��![]() ʱ��
ʱ��
��![]()
��![]()
������������![]() ��
��![]() ��
��![]() ʱ������
ʱ������![]() ��
��![]() �������ߣ�
�������ߣ�

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�