题目内容
【题目】等腰三角形周长为8
，底边BC长为
,腰AB长为
,
(1)写出
关于
的函数关系式__________________；
(2)写出
的取值范围_____________；写出
的取值范围_____________．
(3)画出这个函数的图象．
【答案】 y=8-2x 2<x<4 0<y<4
【解析】试题分析：（1）根据：底边长+两腰长=周长，建立等量关系，变形即可；
（2）根据三角形两边之和大于第三边，即可确定自变量的取值范围，根据函数解析式，可得y的取值范围；
（3）根据函数关系式及其性质，结合自变量的取值范围即可画出图象．
试题解析：解：（1）根据题意，得：2x+y=8，则y=8﹣2x．
故y随x变化的函数关系式为y=8﹣2x；
（2）根据三角形的三边关系得： 
．∵y=8﹣2x，∴
，解得：2＜x＜4，∴-8＜-2x＜-4，0＜8-2x＜4，即0＜y＜4．
故自变量x的取值范围是：2＜x＜4，y的取值范围是：0＜y＜4；
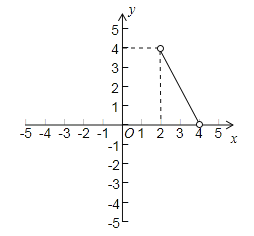
（3）函数y=8﹣2x（2＜x＜4）的图象为：
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
