题目内容
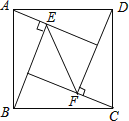
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A. 7 B. 8 C. 7![]() D. 7
D. 7![]()
【答案】C
【解析】试题解析:
如图所示:
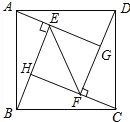
∵四边形ABCD是正方形,
![]()
![]()
在△ABE和△CDF中,
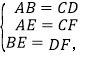
∴△ABE≌△CDF(SSS),
∴∠ABE=∠CDF,
![]()
![]()
∴∠ABE=∠DAG=∠CDF,
同理:∠ABE=∠DAG=∠CDF=∠BCH,
![]() 即
即![]()
同理:![]()
在△ABE和△ADG中,
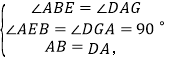 ∴△ABE≌△ADG(AAS),
∴△ABE≌△ADG(AAS),
∴AE=DG,BE=AG,
同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,
∴EG=GF=FH=EF=125=7,
![]() ∴四边形EGFH是正方形,
∴四边形EGFH是正方形,
![]()
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.