题目内容
【题目】如图,E是△ABC中BC边上的一点,且BE= ![]() BC;点D是AC上一点,且AD=
BC;点D是AC上一点,且AD= ![]() AC,S△ABC=24,则S△BEF﹣S△ADF=( )
AC,S△ABC=24,则S△BEF﹣S△ADF=( ) 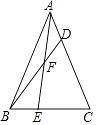
A.1
B.2
C.3
D.4
【答案】B
【解析】解:过D作DG∥AE交CE于G, ∵AD= ![]() AC,
AC,
∴CG=3EG,
∴AE= ![]() DG,CE=
DG,CE= ![]() CG,
CG,
∵EC=2BE,
∴BE=2EG,
∴EF= ![]() DG,
DG,
∴AF= ![]() DG,
DG,
∴EF=AF,
∵S△ABC=24,
∴S△ABD= ![]() S△ABC=6.
S△ABC=6.
∵EC=2BE,S△ABC=24,
∴S△ABE= ![]() S△ABC=8,
S△ABC=8,
∵S△ABE﹣S△ABD=(S△ABF+S△BEF)﹣(S△ADF+S△ABF)=S△BEF﹣S△ADF ,
即S△BEF﹣S△ADF=S△ABE﹣S△ABD=8﹣6=2.
故选B.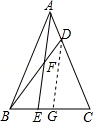
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目