题目内容
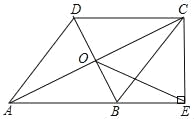
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,正方形
,正方形![]() 的边长为2,将正方形
的边长为2,将正方形![]() 绕点
绕点![]() 旋转一周,连接
旋转一周,连接![]() 、
、![]() 、
、![]() .
.
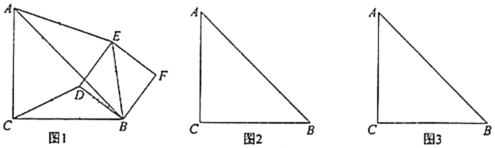
(1)猜想:![]() 的值是__________,直线
的值是__________,直线![]() 与直线
与直线![]() 相交所成的锐角度数是__________;
相交所成的锐角度数是__________;
(2)探究:直线![]() 与
与![]() 垂直时,求线段
垂直时,求线段![]() 的长;
的长;
(3)拓展:取![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出线段
,直接写出线段![]() 长的取值范围.
长的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)(3)
;(3)(3)![]() .
.
【解析】
(1)证明△CBD∽△ABE,相似比为![]() ,△ABE可以看做△CBD绕点B逆时针旋转45°后放大
,△ABE可以看做△CBD绕点B逆时针旋转45°后放大![]() 得到,故直线
得到,故直线![]() 与直线
与直线![]() 相交所成的锐角度数是45°;
相交所成的锐角度数是45°;
(2)证明![]() ,得到
,得到![]() ,分点
,分点![]() 在线段
在线段![]() 上和点
上和点![]() 在线段
在线段![]() 延长线上两类讨论,分别求出AE长,即可求出CD;
延长线上两类讨论,分别求出AE长,即可求出CD;
(3)延长EF到G使得FG=EF,连接AG,BG,则△BFG为等腰直角三角形,求出BG,证明MF=![]() ,根据三角形三边关系求出AG取值范围,问题得解.
,根据三角形三边关系求出AG取值范围,问题得解.
解:(1)由题意得,△ABC, △EBD都是等腰直角三角形,
∴![]() ,
,![]()
∴![]()
∴△CBD∽△ABE
∴![]() ,△ABE可以看做△CBD绕点B逆时针旋转45°后放大
,△ABE可以看做△CBD绕点B逆时针旋转45°后放大![]() 得到,故直线
得到,故直线![]() 与直线
与直线![]() 相交所成的锐角度数是45°;
相交所成的锐角度数是45°;
(2)∵![]() 是腰长为4的等腰直角三角形,四边形
是腰长为4的等腰直角三角形,四边形![]() 的边长为2的正方形,
的边长为2的正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() ,∴当
,∴当![]() 时,
时,![]() 、
、![]() 、
、![]() 三点在一直线上时,
三点在一直线上时,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
如图2,当点![]() 在线段
在线段![]() 上时,
上时,![]() ,∴
,∴![]() ;
;
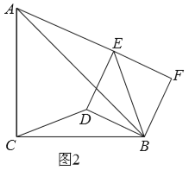
如图3,当点![]() 在线段
在线段![]() 延长线上时,
延长线上时,![]() ,∴
,∴![]() .
.
综上所述,当![]() 时,线段
时,线段![]() 的长为
的长为![]() 或
或![]() ;
;

(3)延长EF到G使得FG=EF,连接AG,BG,
则△BFG为等腰直角三角形,
∴BG=![]() BF=
BF=![]() ,
,
∵M为AE中点,F为EG中点,
∴MF为△EAG中位线,
∴MF=![]() ,
,
在△ABG中,∵AB-BG≤AG≤AB+BG,
∴![]() ≤AG≤
≤AG≤![]() ,
,
∴![]() ≤MF≤
≤MF≤![]() .
.
本题为相似的综合题,考查了相似三角形的判定和性质,正方形,等腰直角三角形的性质,三角形中位线定理,三角形三边关系,解题关键是找到图形中的旋转相似,注意运用好分类讨论的数学思想,问题3中要善于构造中位线解决问题.

【题目】为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,做好师生返校前的卫生安全防护教育,上好开学第一课,省教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七、八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:
收集数据
八年级:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
七年级:
80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
整理数据
成绩 |
|
|
|
|
八年级 | 2 | 5 |
|
|
七年级 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
八年级 | 85.75 | 87.5 |
|
七年级 | 83.5 |
| 80 |
应用数据
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)看完统计数据,你认为对新型冠状病毒肺炎防护知识掌握更好的年级是__________;
(3)若八年级共有500人参与答卷,请估计八年级成绩大于90分的人数;
(4)在这次测试中,八年级学生甲与七年级学生乙的成绩都是85分,请判断两人在各自年级的排名谁更靠前,并说明理由.