题目内容
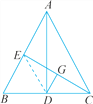
【题目】如图,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于点G,求证:
(1)G是CE的中点.
(2)∠B=2∠BCE.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)如图,连接DE,由AD是△ABC的高,CE是△ABC的中线可证DE=![]() AB=BE,结合DC=BE可得DE=DC,由此可得△DEC是等腰三角形,由DG⊥CE可得G为CE的中点;
AB=BE,结合DC=BE可得DE=DC,由此可得△DEC是等腰三角形,由DG⊥CE可得G为CE的中点;
(2)由(1)的证明可知DE=DC,BE=DE,由此可得∠B=∠EDB,∠DEC=∠DCE,再由∠EDB=∠DEC+∠DCE可得结论.
试题解析:
(1)如图,连结DE.
∵AD是高线,
∴△ABD是直角三角形.
∵CE是AB边上的中线,
∴DE是Rt△ABD斜边上的中线.
∴DE=BE.
∵DC=BE,
∴DE=DC.
又∵DG⊥CE,
∴CG=EG,即G是CE的中点.
(2)∵DE=BE,
∴∠B=∠BDE.
∵DE=DC,
∴∠DEC=∠BCE.
∵∠BDE是△DCE的一个外角,
∴∠BDE=∠DEC+∠BCE=2∠BCE.
∴∠B=2∠BCE.

练习册系列答案
相关题目