题目内容
【题目】为参加运动会，某市射击队组织甲、乙、丙三名运动员进行射击测试，每人射击10次，其测试成绩如表：
甲的测试成绩表
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩（环） | 8 | 6 | 8 | 7 | 8 | 8 | 9 | 9 | 9 | 8 |
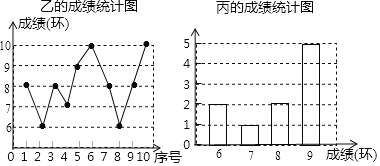
请根据以上图表解决下列问题：
（1）乙运动员测试成绩的众数是 环；丙运动员测试成绩的中位数是 环；
（2）若从三人中选拔一名成绩最稳定的运动员参加本次运动会，你认为选谁更合适？请通过计算明．（参考数据：已知S乙2＝1.8，S丙2＝1.4）
（3）若准备从甲、乙、丙三人中任意选取两人组合参加团体比赛，由于三人的平均成绩相同，因此三人都符合条件，为了保证公平竞争，现采取抽签的方式产生，请用画树状图或列表格的方法求出选中甲、乙组合的概率是多少？
【答案】（1）8，8.5；（2）成绩最稳定的运动员是甲，应选甲参加本次运动会；（3）
．
【解析】
（1）根据众数和中位数的定义直接求解即可；
（2）先求出甲的方差，再与乙和丙进行比较，即可得出答案；
（3）根据题意先画出树状图得出所有等情况数和甲、乙组合的情况数，然后根据概率公式求解即可．
（1）∵8环出现了4次，出现的次数最多，
∴乙运动员测试成绩的众数是8环；
把丙运动员测试成绩按从小到大排列，则中位数是
＝8.5（环），
故答案为：8，8.5；
（2）甲的平均数是：
（8+6+8+7+8+8+9+9+9+8）＝8（环），
则方差是：[5（8﹣8）2+（6﹣8）2+（7﹣8）2+3（9﹣8）2]＝0.8，
∵S乙2＝1.8，S丙2＝1.4，
∴成绩最稳定的运动员是甲，应选甲参加本次运动会；
（3）画树状图如下：
共有6种等情况数，其中甲、乙组合的有2种，
则选中甲、乙组合的概率是
．
练习册系列答案
相关题目
