��Ŀ����
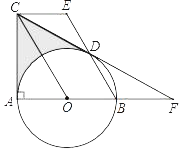
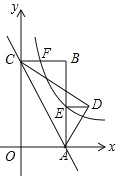
����Ŀ����ͼ1��������y��ax2+bx+4��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y��2����������������D��E����֪��D��E�ĺ�����ֱ�Ϊx1��x2������x1+x2��3��ֱ��BC�ı���ʽΪy����x+n��
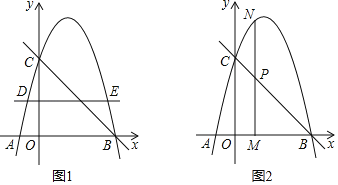
��1����n��ֵ�������ߵı���ʽ��
��2�����Q��ֱ��DE��һ���㣬�ʣ���Q��ʲôλ����ʱ����QOB���ܳ���С�������Q�����꼰��QOB�ܳ�����Сֵ��
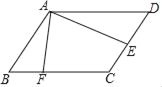
��3����ͼ2��M���߶�OB�ϵ�һ�����㣬����M����ֱ��x���ֱ����ֱ��BC�������߷ֱ��ڵ�P��N������F��ֱ��BC��һ�����㣬����Pǡ�����߶�MN���е�ʱ��������ƽ�����Ƿ���ڵ�G��ʹ�Ե�G��F��P��MΪ������ı��������Σ������ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+3x+4;��2��4![]() +4;��3������,G����Ϊ��
+4;��3������,G������![]() ����
����![]() ����
����![]() ����
����
��������
��1���������߹���C����C�����꣬��ֱ��Ҳ����C�����n��ֵ���õ�n��ֵ����ֱ��BC�Ĺ�ϵʽ��������BC��x�ύ��B�����꣬����DE��x���������������x1+x2��3�����õ������߶Գ��ᩁ![]() ���ٰѵ�B������������߹�ϵʽ�÷����飬���a��b��ֵ���ɣ�
���ٰѵ�B������������߹�ϵʽ�÷����飬���a��b��ֵ���ɣ�
��2�����ڵ�Q��ֱ��y��2���˶���Ҫ�����OQ+BQ����Сֵ��O��B�Ƕ��㣬��Ѱ��O��B����ֱ��y��2�ĶԳƵ㣮��C��0��4����C��O����ֱ��y��2�Գƣ�����CQ��OQ������C��Q��B��ͬһֱ����ʱ����Сֵ����ֱ��BC��y��2ʱ�ĺ����꣬��ΪQ�����꣮����BC��OB�ĺͼ�Ϊ��QOB�ܳ���Сֵ��
��3���ȸ����������M��P��N���꣬����PΪMN�е�ĵ�����ϵ�����P��M���꣮�ٶ������ĸ�����λ�������ۣ�����PMΪ���εıߣ���ʱ�ַ�����������ֱ��ǵ�F�ڵ�P���Ҳ�����ۣ���F��P���ʱ�������������ʺ�GM��x��н�Ϊ45������G�����ꣻ��F��P�Ҳ�ʱ�����ݶԳ��Լ����G�����꣮����PMΪ���ζԽ��ߣ����öԽ����ഹֱƽ�ֵ����ʼ������G���꣮
��1����x��0ʱ��������y��ax2+bx+4��4��
��C��0��4����
�ߵ�C��ֱ��BC��y����x+n�ϣ�
��n��4��
��ֱ��BC��x�ύ��ΪB����x+4��0����ã�x��4��
��B��4��0����
�ߵ�B���������ϣ�
��16a2+4b+4��0 ��
��yD��yE��2��
��DE��x�ᣬ��D��E���������߶Գ���Գƣ�
��x1+x2��3��
�������߶Գ���Ϊ��ֱ��x��![]() ��
��![]() ��
��
��![]() ��
��
�������̢٢ڽ�ã�![]() ��
��
�������ߵı���ʽΪy����x2+3x+4��
��2������CQ����ͼ1��
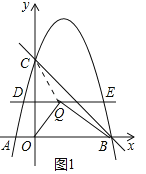
��C��0��4������Q��ֱ��y��2��һ���㣬
��O��C����ֱ��y��2�Գƣ�
��CQ��OQ��
�൱��C��Q��B��ͬһֱ����ʱ��OQ+BQ��CQ+BQ��BC��̣�
����x+4��2ʱ����ã�x��2��
���ʱ��Q��2��2����
��OB��OC��4��
��BC��![]() ��
��
���QOB�ܳ���СֵΪ��C��QOB��OQ+BQ+OB��BC+OB��4![]() +4��
+4��
��3���������������ĵ�G��
��M��m��0����0��m��4������P��m����m+4����N��m����m2+3m+4����
�ߵ�P��MN�е㣬
��MN��2PM��
�ੁm2+3m+4��2����m+4����
��ã�m1��1��m2��4����ȥ����
��M��1��0����P��1��3����PM��3��
����PMΪ���εıߣ�����GFPM�У���F�ڵ�P��࣬��ͼ2���ӳ�FG��x���ڵ�H��
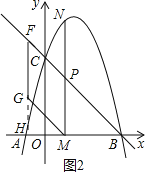
��FP��PM��FG��GM��3��FG��PM��FG��GM��
���GHM��90������GMH����CBO��45����
��MH��GH��![]() GM��
GM��![]() ��
��
��xG��xM��![]() ��
��![]() ��yG��GH��
��yG��GH��![]() ��
��
��G��![]() ��
��![]() ����
����
����PMΪ���εıߣ�����GFPM�У���F�ڵ�P�Ҳ࣬��ͼ3��
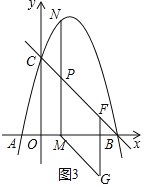
������ͼ2�ĶԳƹ�ϵ�ɵ�G��![]() ����
����![]() ��
��
����PMΪ���εĶԽ��ߣ�����GPFM�У���ͼ4��
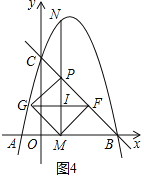
��PM��GF���ڵ�I��
��PI��MI��![]() PM��
PM��![]() ��GI��IF��PM��GF��
��GI��IF��PM��GF��
��GF��x�ᣬyF��yI��yG��![]() ��
��
���PFI����CBO��45����
��GI��IF��PI��![]() ��
��
��xG��xI��![]() ����
����![]() ��
��
��G����![]() ��
��![]() ����
����
�������������������ĵ�G����Ϊ��![]() ����
����![]() ����
����![]() ����
����

 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�����Ŀ��Ϊ�μ��˶��ᣬij���������֯�ס��ҡ��������˶�Ա����������ԣ�ÿ�����10�Σ�����Գɼ������
�IJ��Գɼ���
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ������� | 8 | 6 | 8 | 7 | 8 | 8 | 9 | 9 | 9 | 8 |
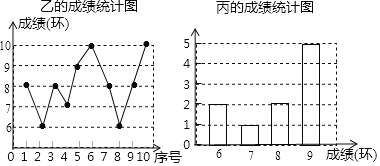
���������ͼ������������⣺
��1�����˶�Ա���Գɼ����������� ���������˶�Ա���Գɼ�����λ������ ������
��2������������ѡ��һ���ɼ����ȶ����˶�Ա�μӱ����˶��ᣬ����Ϊѡ˭�����ʣ���ͨ�������������ο����ݣ���֪S��2��1.8��S��2��1.4��
��3�������Ӽס��ҡ�������������ѡȡ������ϲμ�����������������˵�ƽ���ɼ���ͬ��������˶�����������Ϊ�˱�֤��ƽ�������ֲ�ȡ��ǩ�ķ�ʽ���������û���״ͼ���б���ķ������ѡ�мס�����ϵĸ����Ƕ��٣�