题目内容
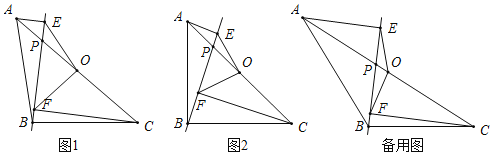
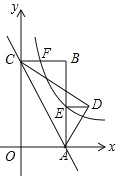
【题目】如图:在四边形纸片ABCD中,AB=12,CD=2,AD=BC=6,∠A=∠B.现将纸片沿EF折叠,使点A的对应点A'落在AB边上,连接A'C.若△A'BC恰好是以A'C为腰的等腰三角形,则AE的长为_____.
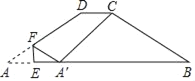
【答案】1或![]() .
.
【解析】
过点C作CM⊥AB于点M,过点D作DN⊥AB于点N,由“AAS”可证△ADN≌△BCM,可得AN=BM,DN=CM,即可证四边形DCMN是矩形,可得CD=MN=2,AN=BM=5,由折叠性质可得AE=A'E,分A'C=BC和A'C=A'B两种情况讨论,由等腰三角形的性质和勾股定理可求解.
解:如图,过点C作CM⊥AB于点M,过点D作DN⊥AB于点N,
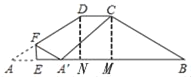
![]()
![]()
![]()
∴四边形DCMN是矩形
![]()
∴AN=BM=![]() =5
=5
∵将纸片沿EF折叠,使点A的对应点A'落在AB边上,
∴AE=A'E,
若A'C=BC,且CM⊥AB
∴BM=A'M=5
∴AA'=AB﹣A'B=12﹣10=2
∴AE=1
若A'C=A'B,过点A'作A'H⊥BC,
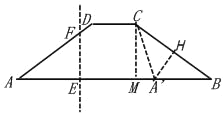
∵CH2=BC2﹣BM2=A'C2﹣A'M2,
∴36﹣25=A'B2﹣(5﹣A'B)2,
∴A'B=![]()
∴AA'=AB﹣A'B=12﹣![]() =
=![]()
∴AE=![]()
故答案为:1或![]()

【题目】为参加运动会,某市射击队组织甲、乙、丙三名运动员进行射击测试,每人射击10次,其测试成绩如表:
甲的测试成绩表
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(环) | 8 | 6 | 8 | 7 | 8 | 8 | 9 | 9 | 9 | 8 |
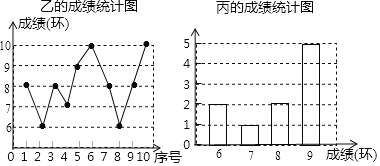
请根据以上图表解决下列问题:
(1)乙运动员测试成绩的众数是 环;丙运动员测试成绩的中位数是 环;
(2)若从三人中选拔一名成绩最稳定的运动员参加本次运动会,你认为选谁更合适?请通过计算明.(参考数据:已知S乙2=1.8,S丙2=1.4)
(3)若准备从甲、乙、丙三人中任意选取两人组合参加团体比赛,由于三人的平均成绩相同,因此三人都符合条件,为了保证公平竞争,现采取抽签的方式产生,请用画树状图或列表格的方法求出选中甲、乙组合的概率是多少?