题目内容
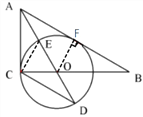
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() .
.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,设⊙
)的条件下,设⊙![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
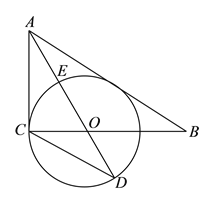
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:对于(1),过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;
对于(2),连接CE,结合角平分线的性质和弦切角定理可证明△ACE∽△ADC,可得![]() =tanD,即可解答;
=tanD,即可解答;
对于(3),先由勾股定理求得AE的长,再证明△BOF∽△BAC,得![]() ,设BO=y,BF=z,列二元一次方程组即可解决问题.
,设BO=y,BF=z,列二元一次方程组即可解决问题.
试题解析:( ![]() )证明:作
)证明:作![]() 于
于![]() ,
,
∵![]() 是
是![]() 的角平分线,
的角平分线, ![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )连接
)连接![]() ,
,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() 所对的弧于
所对的弧于![]() 所对的弧是同弧,
所对的弧是同弧,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )设
)设![]() ,在
,在![]() 中,
中,
由勾股定理得![]() ,解得
,解得![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() ,
, ![]() .
.
∴![]() .
.

练习册系列答案
相关题目