题目内容
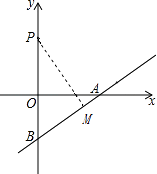
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= ![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
A.3
B.4
C.5
D.6
【答案】B
【解析】解:如图,过点P作PM⊥AB,则:∠PMB=90°,当PM⊥AB时,PM最短,
∵直线y= ![]() x﹣3与x轴、y轴分别交于点A,B,
x﹣3与x轴、y轴分别交于点A,B,
∴点A的坐标为(4,0),点B的坐标为(0,﹣3),
在Rt△AOB中,AO=4,BO=3,AB= ![]() =5,
=5,
∵∠BMP=∠AOB=90°,∠B=∠B,PB=OP+OB=5,
∴△PBM∽△ABO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得:PM=4.
,解得:PM=4.
所以答案是:B.
【考点精析】通过灵活运用垂线段最短和勾股定理的概念,掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |