题目内容
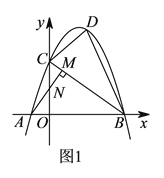
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点, ![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
(![]() )求抛物线的函数式.
)求抛物线的函数式.
(![]() )连接
)连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
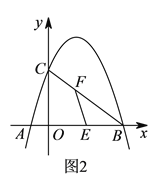
【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)此时
;(3)此时![]() ,
, ![]() .
.
【解析】试题分析:(1)先证明△AON∽△COB,利用相似比计算出OA=1,得到A(-1,0),然后利用交点式可求出抛物线解析式为y=-![]() x2+
x2+![]() x+3;
x+3;
(2)先利用待定系数法求出直线BC的解析式为y=-![]() x+3,作PQ∥y轴交BC于Q,如图1,设P(x,-
x+3,作PQ∥y轴交BC于Q,如图1,设P(x,-![]() x2+
x2+![]() x+3),则Q(x,-
x+3),则Q(x,-![]() x+3),再计算出DQ=-
x+3),再计算出DQ=-![]() x2+3x,根据三角形面积公式得S△BCD=S△CDQ+S△BDQ=-
x2+3x,根据三角形面积公式得S△BCD=S△CDQ+S△BDQ=-![]() x2+6x,然后根据S△BCD=
x2+6x,然后根据S△BCD=![]() S△ABC得到-
S△ABC得到-![]() x2+6x=
x2+6x=![]() ×
×![]() ×(4+1)×3,然后解方程求出x即可得到D点坐标;
×(4+1)×3,然后解方程求出x即可得到D点坐标;
(3)过![]() 做
做![]() 平行
平行![]() 轴交抛物线于
轴交抛物线于![]() ,过
,过![]() 做
做![]() ,可证
,可证![]() ,由此
,由此![]() ,过
,过![]() 作
作![]() 的垂线,交点即为
的垂线,交点即为![]() 点,可得
点,可得![]() 值和点
值和点![]() 坐标.
坐标.
试题解析:( ![]() )
)![]() ,
,
![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() .
.
设抛物线解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
∴抛物线解析式为![]() .
.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
, ![]() 代入得
代入得![]() ,
,
解得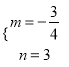 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
作![]() 轴交
轴交![]() 于
于![]() ,如图1,设
,如图1,设
![]() ,则
,则![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,解得
,解得![]() ,
, ![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
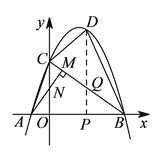
(![]() )设运动时间为
)设运动时间为![]() ,则
,则
![]() ,
,
![]() ,
,
过![]() 做
做![]() 平行
平行![]() 轴交抛物线于
轴交抛物线于![]() ,过
,过![]() 做
做![]() ,
,
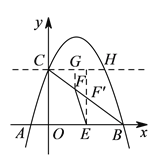
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
过![]() 作
作![]() 的垂线,交点即为
的垂线,交点即为![]() 点,
点,
此时![]() ,
,
![]() .
.

练习册系列答案
相关题目