题目内容
已知抛物线y=ax2+(
+3a)x+4与x轴交于A、B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形?若存在,请求出a的值;若不存在,请说明理由.
| 4 |
| 3 |
依题意,得点C的坐标为(0,4),
设点A、B的坐标分别为(x1,0),(x2,0),
由ax2+(
+3a)x+4=0,
解得x1=-3,x2=-
,
∴点A、B的坐标分别为(-3,0),(-
,0),
∴AB=|-
+3|,AC=
=5,BC=
=
,
∴AB2=|-
+3|2=
-
+9,
AC2=25,BC2=
+16.
(ⅰ)当AB2=AC2+BC2时,∠ACB=90°,
由AB2=AC2+BC2,
得
-
+9=25+
+16,
解得a=-
,
∴当a=-
时,点B的坐标为(
,0),
AB2=
,AC2=25,BC2=
,
于是AB2=AC2+BC2,
∴当a=-
时,△ABC为直角三角形.
(ⅱ)当AC2=AB2+BC2时,∠ABC=90°,
由AC2=AB2+BC2,
得25=
-
+9+
+16,
解得a=
.
当a=
时,-
=-
=-3,点B(-3,0)与点A重合,不合题意.
<ⅲ>当BC2=AC2+AB2时,∠BAC=90°,
由BC2=AC2+AB2,
得25+
-
+9=
+16,
解得a=
,
不合题意.
综合<ⅰ>、<ⅱ>、<ⅲ>,当a=-
时,△ABC为直角三角形.
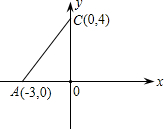
设点A、B的坐标分别为(x1,0),(x2,0),
由ax2+(
| 4 |
| 3 |
解得x1=-3,x2=-
| 4 |
| 3a |
∴点A、B的坐标分别为(-3,0),(-
| 4 |
| 3a |
∴AB=|-
| 4 |
| 3a |
| AO2+OC2 |
| CB2+OC2 |
|-
|
∴AB2=|-
| 4 |
| 3a |
| 16 |
| 9a2 |
| 8 |
| a |
AC2=25,BC2=
| 16 |
| 9a2 |
(ⅰ)当AB2=AC2+BC2时,∠ACB=90°,
由AB2=AC2+BC2,
得
| 16 |
| 9a2 |
| 8 |
| a |
| 16 |
| 9a2 |
解得a=-
| 1 |
| 4 |
∴当a=-
| 1 |
| 4 |
| 16 |
| 3 |
AB2=
| 625 |
| 9 |
| 400 |
| 9 |
于是AB2=AC2+BC2,
∴当a=-
| 1 |
| 4 |
(ⅱ)当AC2=AB2+BC2时,∠ABC=90°,
由AC2=AB2+BC2,
得25=
| 16 |
| 9a2 |
| 8 |
| a |
| 16 |
| 9a2 |
解得a=
| 4 |
| 9 |
当a=
| 4 |
| 9 |
| 4 |
| 3a |
| 4 | ||
3×
|
<ⅲ>当BC2=AC2+AB2时,∠BAC=90°,
由BC2=AC2+AB2,
得25+
| 16 |
| 9a2 |
| 8 |
| a |
| 16 |
| 9a2 |
解得a=
| 4 |
| 9 |
不合题意.
综合<ⅰ>、<ⅱ>、<ⅲ>,当a=-
| 1 |
| 4 |

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目