题目内容
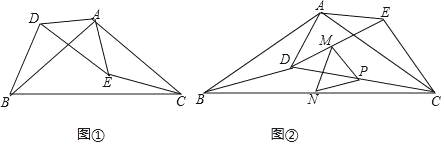
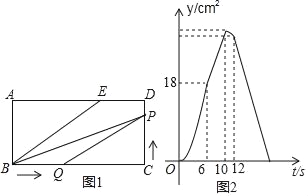
【题目】如图1,E为矩形ABCD边AD上一点,点P从点C沿折线CD﹣DE﹣EB运动到点B时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
A.AE=8cm
B.sin∠EBC=![]()
C.当10≤t≤12时,![]()
D.当t=12s时,△PBQ是等腰三角形
【答案】D
【解析】
观察图象可知:点P在CD上运动的时间为6s,在DE上运动的时间为4s,点Q在BC上运动的时间为12s,所以CD=6,DE=4,BC=12,然后结合三角函数、三角形的面积等逐一进行判断即可得.
观察图象可知:点P在CD上运动的时间为6s,在DE上运动的时间为4s,点Q在BC上运动的时间为12s,
所以CD=6,DE=4,BC=12,
∵AD=BC,
∴AD=12,
∴AE=12﹣4=8cm,故A正确,
在Rt△ABE中,∵AE=8,AB=CD=6,
∴BE=![]() =10,
=10,
∴sin∠EBC=sin∠AEB=![]() ,故B正确,
,故B正确,
当10≤t≤12时,点P在BE上,BP=10﹣(t﹣10)=20﹣t,
∴S△BQP=![]() t(20﹣t)
t(20﹣t)![]() =﹣
=﹣![]() t2+6t,故C正确,
t2+6t,故C正确,
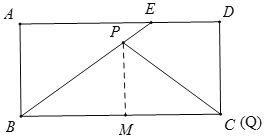
如图,当t=12时,Q点与C点重合,点P在BE上,此时BP=20-12=8,过点P作PM⊥BC于M,
在Rt△BPM中,cos∠PBM=![]() ,
,
又∠PBM=∠AEB,在Rt△ABE中,cos∠AEB=![]() ,
,
∴![]() ,
,
∴BM=6.4,∴QM=12-6.4=5.6,
∴BP≠PC,即△PBQ不是等腰三角形,故D错误,
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目