题目内容
边长为a的正六边形的边心距等于( )
A.
| B.
| C.a | D.
|
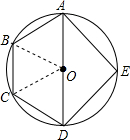
连接OA、OB、OC、OD、OE、OF,
∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴∠AOB=
×360°=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=a,
∵OM⊥AB,
∴AM=BM=
a,
在△OAM中,由勾股定理得:OM=
=
a.
故选:A.
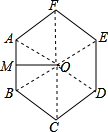
∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴∠AOB=
| 1 |
| 6 |
∴△AOB是等边三角形,
∴OA=OB=AB=a,
∵OM⊥AB,
∴AM=BM=
| 1 |
| 2 |
在△OAM中,由勾股定理得:OM=
| OA2-AM2 |
| ||
| 2 |
故选:A.


练习册系列答案
相关题目