题目内容
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )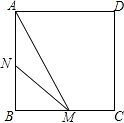
A.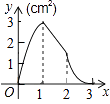
B.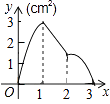
C.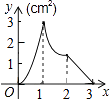
D.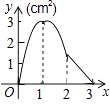
【答案】A
【解析】解:由题可得,BN=x,
当0≤x≤1时,M在BC边上,BM=3x,AN=3﹣x,则
S△ANM= ![]() ANBM,
ANBM,
∴y= ![]() (3﹣x)3x=﹣
(3﹣x)3x=﹣ ![]() x2+
x2+ ![]() x,故C选项错误;
x,故C选项错误;
当1≤x≤2时,M点在CD边上,则
S△ANM= ![]() ANBC,
ANBC,
∴y= ![]() (3﹣x)3=﹣
(3﹣x)3=﹣ ![]() x+
x+ ![]() ,故D选项错误;
,故D选项错误;
当2≤x≤3时,M在AD边上,AM=9﹣3x,
∴S△ANM= ![]() AMAN,
AMAN,
∴y= ![]() (9﹣3x)(3﹣x)=
(9﹣3x)(3﹣x)= ![]() (x﹣3)2 , 故B选项错误;
(x﹣3)2 , 故B选项错误;
故选(A).
分三种情况进行讨论,当0≤x≤1时,当1≤x≤2时,当2≤x≤3时,分别求得△ANM的面积,列出函数解析式,根据函数图象进行判断即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目