��Ŀ����
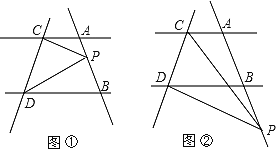
����Ŀ����ͼ,��ֱ֪��AC��BD,ֱ��AB��CD��ƽ��,��P��ֱ��AB��,�Һ͵�A��B���غ�.
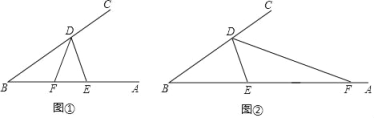
(1)��ͼ�٣�����P���߶�AB��ʱ������PCA=20�㣬��PDB=30�㣬���CPD�Ķ�����
(2)��P��A��B����֮���˶�ʱ����PCA����PDB����CPD֮������ʲô���ĵ�����ϵ(ֱ��д����)��
(3)��ͼ�ڣ�����P���߶�AB���ӳ������˶�ʱ����PCA����PDB����CPD֮������ʲô���ĵ�����ϵ����˵�����ɡ�
���𰸡���1��50�㣨2����CPD=��PCA+��PDB��3����CPD=��PCA-��PDB
��������
��1����ͼ�٣���P����PE��AC��CD��E�㣬����AC��BD����PE��BD������ƽ���ߵ����ʵá�CPE=��PCA=20������DPE=��PDB=30�������ԡ�CPD=50����
��2��֤�������루1��һ����
��3����ͼ�ڣ���P����PF��BD��CD��F�㣬����AC��BD����PF��AC������ƽ���ߵ����ʵá�CPF=��PCA����DPF=��PDB�����ԡ�CPD=��PCA-��PDB��
��1����ͼ�٣���P����PE��AC��CD��E�㣬
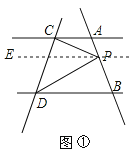
��AC��BD
��PE��BD��
���CPE=��PCA=20������DPE=��PDB=30����
���CPD=��CPE+��DPE=50����
��2����CPD=��PCA+��PDB��֤�������루1��һ������
��3����CPD=��PCA-��PDB���������£�
��ͼ�ڣ���P����PF��BD��CD��F�㣬
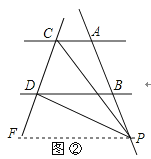
��AC��BD��
��PF��AC��
���CPF=��PCA����DPF=��PDB��
���CPD=��CPF-��DPF=��PCA-��PDB��