题目内容
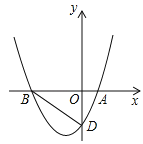
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.
【答案】(1)y=![]() x2+x﹣4;(2)满足条件的P的坐标为(﹣1,﹣2+
x2+x﹣4;(2)满足条件的P的坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() );(3)满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+
);(3)满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+![]() ,4).
,4).
【解析】(1)、利用待定系数法求出函数解析式;(2)、分BD为矩形的边和BD为矩形的对角线两种情况分别求出点P的坐标;(3)、设M(m,![]() m2+m﹣4),设直线AM的解析式为y=kx+b,然后求出直线AM的解析式,然后分点M所在的象限,证明出△MNB和△BOC相似,从而分别得出点M的坐标.
m2+m﹣4),设直线AM的解析式为y=kx+b,然后求出直线AM的解析式,然后分点M所在的象限,证明出△MNB和△BOC相似,从而分别得出点M的坐标.
(1)、由题意![]() ,解得
,解得![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2+x﹣4.
x2+x﹣4.
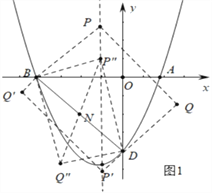
(2)如图1中,当BD为矩形的边时,∵直线BD的解析式为y=﹣x﹣4,
∴直线BP的解析式为y=x=4,直线 DP′的解析式为y=x﹣4,
可得P(﹣1,3),P′(﹣1,﹣5).
当BD为矩形的对角线时,设P(﹣1,m),BD的中点N(﹣2,﹣2),由BN=P″N,
可得12+(m+2)2=(2![]() )2, 解得m=﹣2+
)2, 解得m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]() ,
,
∴P″(﹣1,﹣2+![]() ),或(﹣1.﹣2﹣
),或(﹣1.﹣2﹣![]() ),
),
∴要使四边形PBQD能成为矩形,满足条件的点P坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() ).
).
综上所述,满足条件的P的坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() ).
).
(3)设M(m,![]() m2+m﹣4),设直线AM的解析式为y=kx+b,则有
m2+m﹣4),设直线AM的解析式为y=kx+b,则有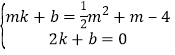 ,
,
解得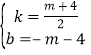 ,∴直线AM的解析式为y=
,∴直线AM的解析式为y=![]() x﹣m﹣4,∴C(0,﹣m﹣4).
x﹣m﹣4,∴C(0,﹣m﹣4).
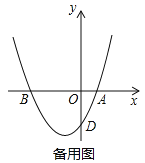
①点M在第二象限显然不可能,当点M在第三象限时,如图2中,作MN⊥OB于N.
∵∠MBN=∠BCO,∠MNB=∠BOC=90°,∴△MNB∽△BOC,∴![]() ,
,
∴![]() =
=![]() ,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4).
,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4).
②当点M在第一象限时,同法可得![]() =
=![]() ,整理得:m2+2m﹣16=0,
,整理得:m2+2m﹣16=0,
∴m=﹣1+![]() 或﹣1﹣
或﹣1﹣![]() (舍弃),∴M(﹣1+
(舍弃),∴M(﹣1+![]() ,4),
,4),
③当点M在第四象限时,不存在,
综上所述,满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+![]() ,4).
,4).


 阅读快车系列答案
阅读快车系列答案