题目内容
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
【答案】
(1)解:∵二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3),
∴ ![]() ,解得
,解得 ![]() ,
,
∴此二次函数的表达式为y=﹣x2+4x﹣3;
y=﹣x2+4x﹣3=﹣(x﹣2)2+1
(2)解:∵y=﹣(x﹣2)2+1,
∴顶点坐标为(2,1),对称轴方程为x=2.
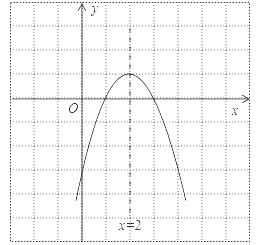
∵函数二次函数y=﹣x2+4x﹣3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为
【解析】(1)利用待定系数法将已知点的坐标代入函数解析式,建立方程组,求出b、c的值,可得到而此函数解析式,再将其通过配方化成顶点式。
(2)先根据函数解析式求出抛物线与x轴的两交点坐标,再根据顶点坐标及抛物线的开口方向,画出函数图像。
【考点精析】通过灵活运用二次函数的图象和抛物线与坐标轴的交点,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.

练习册系列答案
相关题目