题目内容
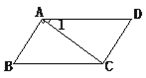
【题目】如图1所示，从边长为a的正方形纸片中减去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形（其面积= 
）.
（1）设图1中阴影部分面积为S1，图2中阴影部分面积为S2，请直接用含a、b的式子表示S1和S2；
（2）请写出上述过程所揭示的乘法公式．
【答案】（1）
， 
；（2）
.
【解析】试题分析：（1）先用大正方形的面积减去小正方形的面积，即可求出S1，再根据梯形的面积公式即可求出S2；
（2）根据（1）得出的值，直接可写出乘法公式（a+b）（a-b）=a2-b2．
试题解析：（1）∵大正方形的边长为a，小正方形的边长为b，
∴S1=a2﹣b2，
S2=
（2a+2b）（a﹣b）=（a+b）（a﹣b）；
（2）根据题意得：
（a+b）（a﹣b）=a2﹣b2.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了保护环境，某企业决定购买10台污水处理设备；现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：
A型 | B型 | |
价格（万元/台） | 12 | 10 |
处理污水量（吨/月） | 240 | 200 |
年消耗费（万元/台） | 1 | 1 |
经预算，该企业购买设备的资金不高于105万元。
（1） 请你设计该企业有几种购买方案；
（2）若该企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案？
