题目内容
【题目】定义：在平面直角坐标系中，图形G上点P(x，y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”，记作Zp，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”．
(1)①点A(3，1)的“坐标差”为_______；
②抛物线y＝﹣x2+5x的“特征值”为________；
(2)某二次函数y＝﹣x2+bx+c(c≠0)的“特征值”为﹣1，点B(m，0)与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等．
①直接写出m＝______；(用含c的式子表示)
②求此二次函数的表达式．
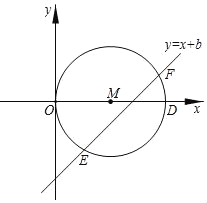
(3)如图，在平面直角坐标系xOy中，点D(4，0)，以OD为直径作⊙M，直线y＝x+b与⊙M相交于点E、F．
①比较点E、F的“坐标差”ZE、ZF的大小．
②请直接写出⊙M的“特征值”为_______．
【答案】(1)①-2；②4；(2)①-c；②y＝﹣x2+3x﹣2；(3)①ZE＝ZF；②2
﹣2．
【解析】
（1）①由“坐标差”的定义可求出点A（3，1）的“坐标差”；
②用y﹣x可找出y﹣x关于x的函数关系式，再利用配方法即可求出y﹣x的最大值，进而可得出抛物线y＝﹣x2+5x的“特征值”；
（2）①利用二次函数图象上点的坐标特征可求出点C的坐标，由“坐标差”的定义结合点B与点C的“坐标差”相等，即可求出m的值；
②由点B的坐标利用待定系数法可找出b，c之间的关系，找出y﹣x关于x的函数关系式，再利用二次函数的性质结合二次函数y＝﹣x2+bx+c（c≠0）的“特征值”为﹣1，即可得出关于b的一元二次方程，解之即可得出b的值，进而可得出c的值，此问得解；
（3）①利用一次函数图象上点的坐标特征可设点E的坐标为（xE，xE+b），点F的坐标为（xF，xF+b），结合“坐标差”的定义可得出ZE＝ZF；
②作直线y＝x+n（n＞0）与⊙M相切，设切点为N，该直线与x轴交于点Q，利用等腰直角三角形的性质可求出点Q的坐标，再利用待定系数法可求出n值，结合“特征值”的定义即可找出⊙M的“特征值”．
(1)①1﹣3＝﹣2．
故答案为：﹣2．
②y﹣x＝﹣x2+5x﹣x＝﹣(x﹣2)2+4，
∵﹣1＜0，
∴当x＝2时，y﹣x取得最大值，最大值为4．
故答案为：4．
(2)①当x＝0时，y＝﹣x2+bx+c＝c，
∴点C的坐标为(0，c)．
∵点B与点C的“坐标差”相等，
∴0﹣m＝c﹣0，
∴m＝﹣c．
故答案为：﹣c．
②由①可知：点B的坐标为(﹣c，0)．
将点B(﹣c，0)代入y＝﹣x2+bx+c，得：0＝﹣c2﹣bc+c，
∴c1＝1﹣b，c2＝0(舍去)．
∵二次函数y＝﹣x2+bx+c(c≠0)的“特征值”为﹣1，
∴y﹣x＝﹣x2+(b﹣1)x+1﹣b的最大值为﹣1，
∴
=-1，
解得：b＝3，
∴c＝1﹣b＝﹣2，
∴二次函数的解析式为y＝﹣x2+3x﹣2．
(3)①∵点E，F在直线y＝x+b上，
∴设点E的坐标为(xE，xE+b)，点F的坐标为(xF，xF+b)，
∴ZE＝xE+b﹣xE＝b，ZF＝xF+b﹣xF＝b，
∴ZE＝ZF．
②作直线y＝x+n(n＞0)与⊙M相切，设切点为N，该直线与x轴交于点Q，如图所示．
∵y﹣x＝x+n﹣x＝n，
∴当直线y＝x+n(n＞0)与⊙M相切时，y﹣x的值为⊙M的“特征值”．
∵∠NQM＝45°，MN⊥NQ，MN＝2，
∴△MNQ为等腰直角三角形，
∴MQ＝2，
∴点Q的坐标为(2﹣2，0)．
将Q(2﹣2，0)代入y＝x+n，得：0＝2﹣2+n，
解得：n＝2﹣2，
∴⊙M的“特征值”为2﹣2．
故答案为：2﹣2．
