Question

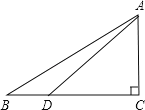
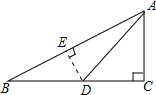
【题目】如图，在Rt△ABC中，∠C＝90°，sinB＝，点D在BC边上，∠ADC＝45°，DC＝6，tan∠BAD＝___．

Answer 1

【答案】.

【解析】

过D点作DE⊥AB，交AB于E点，把构造到直角三角形中，要求的正切值，只需求得DE、AE的长，根据等腰三角形的性质可以求得AC、AD的长，在直角三角形ABC中，根据sinB＝，可以求得AB的长，根据勾股定理进一步求得BC的长，从而求得BD的长，在直角三角形BDE中，根据sinB＝，进一步求得DE的长，根据勾股定理求得BE的长，即可进行计算．

过D点作DE⊥AB，交AB于E点，

在Rt△ADC中，∠C＝90°，∠ADC＝45°，DC＝6，

∴∠DAC＝45°，

∴AC＝DC＝6，

在Rt△ABC中，∠C＝90°，

∵sinB＝，

∴ ＝，

设AC＝3k，则AB＝5k，

∴3k＝6，

∴k＝2，

∴AB＝5k＝10，

根据勾股定理，得BC＝8，

∴BD＝BC﹣DC＝8﹣6＝2

在Rt△BDE中，∠BED＝90°，sinB＝，

∴＝，DE＝，

根据勾股定理，得BE＝，

∴AE＝AB﹣BE＝10﹣＝，

∴tan∠BAD＝＝×＝．