题目内容
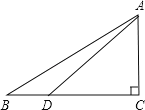
【题目】如图,在直角三角形ABC中,∠C=90°,AC=2,BC=2![]() ,点O是边AB上的一个动点,以点O为圆心,OA为半径作⊙O,与边AC交于点M.
,点O是边AB上的一个动点,以点O为圆心,OA为半径作⊙O,与边AC交于点M.
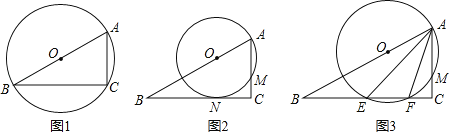
(1)如图1,当⊙O经过点C时,⊙O的直径是 ;
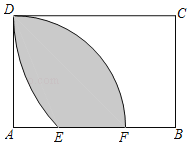
(2)如图2,当⊙O与边BC相切时,切点为点N,试求⊙O与△ABC重合部分的面积;
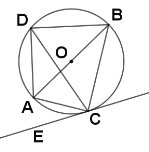
(3)如图3,当⊙O与边BC相交时,交点为E、F,设CM=x,就判断AEAF是否为定值,若是,求出这个定值;若不是,请用含x的代数式表示.
【答案】(1)4;(2)![]() ;(3)不是定值,理由见解析
;(3)不是定值,理由见解析
【解析】
(1)由AB是圆的直径知∠C=90°,再根据勾股定理求解可得;
(2)连结ON,OM,先证tan∠B=![]() 知∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,设ON=OA=r,证△OBN∽△ABC得
知∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,设ON=OA=r,证△OBN∽△ABC得![]() ,据此求出r的值,再计算出2S扇形MON和S△AOM,从而得出答案;
,据此求出r的值,再计算出2S扇形MON和S△AOM,从而得出答案;
(3)设⊙O与AB的另一交点为G,连结GE,OM,证△AGE∽△AFC得![]() ,由AC=2,CM=x知AM=2﹣x,再证∠AOM=60°得OA=AM=2﹣x,AG=2AO=4﹣2x,从而知AEAF=ACAG=8﹣4x,据此得出答案.
,由AC=2,CM=x知AM=2﹣x,再证∠AOM=60°得OA=AM=2﹣x,AG=2AO=4﹣2x,从而知AEAF=ACAG=8﹣4x,据此得出答案.
(1)∵AB是圆的直径,
∴∠C=90°,
∵AC=2,BC=2![]() ,
,
∴AB=4故答案为4;
(2)如图2,连结ON,OM,
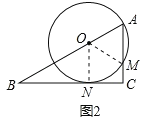
∵⊙O与边BC相切于点N,
∴ON⊥BC
在Rt△ABC中,∠C=90°,AC=2,BC=2![]() ,
,
∴tan∠B=![]() ,
,
∴∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,
∵OA=OM,
∴∠OMA=∠A=60°,
∴∠AOM=60°,∠MON=60°,
设ON=OA=r,
∵∠BNO=∠C=90°,∠B=∠B,
∴△OBN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得r=![]() ,
,
∴2S扇形MON=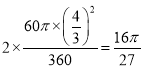 ,
,
∵S△AOM=![]() ,
,
∴⊙O与△ABC重合部分的面积是![]() .
.
(3)AEAF不为定值,理由如下:
如图3,设⊙O与AB的另一交点为G,连结GE,OM,
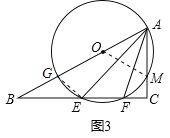
∵AG是⊙O的直径,
∴∠GEA=90°=∠C,
在圆内接四边形AGEF中,∠AGE+∠AFE=180°,
∵∠AFC+∠AFE=180°,
∴∠AGE=∠AFC,
∴△AGE∽△AFC,
∴![]() ,
,
∵AC=2,CM=x,
∴AM=2﹣x,
∵∠OMA=∠OAM=60°,
∴∠AOM=60°,
∴OA=AM=2﹣x,
AG=2AO=4﹣2x,
∴AEAF=ACAG=8﹣4x,
∵x不是定值
∴AEAF不是定值.