题目内容
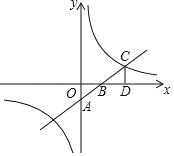
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.

【答案】(1)![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() )(2)①客车和货车的平均速度分别为
)(2)①客车和货车的平均速度分别为![]() 千米/小时和
千米/小时和![]() 千米/小时.②甲地与
千米/小时.②甲地与![]() 加油站的距离为
加油站的距离为![]() 或
或![]() 千米
千米
【解析】
试题(1)利用时间t与速度v成反比例可以得到反比例函数的解析式;
(2)①由客车的平均速度为每小时v千米,得到货车的平均速度为每小时(v-20)千米,根据一辆客车从甲地出发前往乙地,一辆货车同时从乙地出发前往甲地,3小时后两车相遇列出方程,解方程即可;
②分两种情况进行讨论:当A加油站在甲地和B加油站之间时;当B加油站在甲地和A加油站之间时;都可以根据甲、乙两地间有两个加油站A、B,它们相距200千米列出方程,解方程即可.
试题解析:(1)设函数关系式为v=![]() ,
,
∵t=5,v=120,
∴k=120×5=600,
∴v与t的函数关系式为v=![]() (5≤t≤10);
(5≤t≤10);
(2)①依题意,得
3(v+v-20)=600,
解得v=110,
经检验,v=110符合题意.
当v=110时,v-20=90.
答:客车和货车的平均速度分别为110千米/小时和90千米/小时;
②当A加油站在甲地和B加油站之间时,
110t-(600-90t)=200,
解得t=4,此时110t=110×4=440;
当B加油站在甲地和A加油站之间时,
110t+200+90t=600,
解得t=2,此时110t=110×2=220.
答:甲地与B加油站的距离为220或440千米.