题目内容
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG. 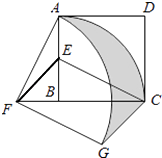
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的 ![]() ,
, ![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
【答案】
(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°,
∵△BEC绕点B逆时针旋转90°得到△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE,
∴∠AFB+∠FAB=90°,
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG,
∵AF=CE,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG
(2)解:∵AD=2,E是AB的中点,
∴BF=BE= ![]() AB=
AB= ![]() ×2=1,
×2=1,
∴AF= ![]() =
= ![]() =
= ![]() ,
,
由平行四边形的性质,△FEC≌△CGF,
∴S△FEC=S△CGF,
∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG,
= ![]() +
+ ![]() ×2×1+
×2×1+ ![]() ×(1+2)×1﹣
×(1+2)×1﹣ ![]() ,
,
= ![]() ﹣
﹣ ![]() .
.
【解析】(1)根据正方形的性质可得AB=BC=AD=2,∠ABC=90°,再根据旋转变化只改变图形的位置不改变图形的形状可得△ABF和△CBE全等,根据全等三角形对应角相等可得∠FAB=∠ECB,∠ABF=∠CBE=90°,全等三角形对应边相等可得AF=EC,然后求出∠AFB+∠FAB=90°,再求出∠CFG=∠FAB=∠ECB,根据内错角相等,两直线平行可得EC∥FG,再根据一组对边平行且相等的四边形是平行四边形判断出四边形EFGC是平行四边形,然后根据平行四边形的对边平行证明;(2)求出FE、BE的长,再利用勾股定理列式求出AF的长,根据平行四边形的性质可得△FEC和△CGF全等,从而得到S△FEC=S△CGF , 再根据S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG列式计算即可得解.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.