Question

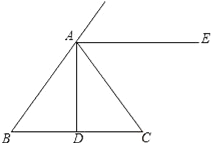
【题目】如图，在△ABC中，AB=AC，D为BC边的中点，AE∥BC．

（1）作∠ADC的平分线DF，与AE交于点F；（用尺规作图，保留作图痕迹，不写作法）

（2）在（1）的条件下，若AD=2，求DF的长．

Answer 1

【答案】（1）作图见解析；

（2）DF的长为．

【解析】试题分析：

（1）尺规作图，作已知角的平分线；

（2）由“角平分线+平行线→等腰三角形”，这个基本图形可得到AD=AF，而∠DAF=90°，则由勾股定理即可得到DF的长.

试题解析：

（1）如图所示：

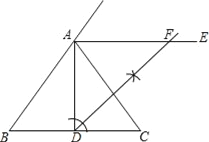
（2）∵AB=AC，D为BC边的中点，

∴AD⊥BC 即∠ADC=90°，

又∵DF平分∠ADC，

∴∠ADF=45°，

又∵AE∥BC，

∴∠DAF=∠ADC=90°，

∴△ADF为等腰直角三角形，

又∵AD=2，

∴DF=2．